Частотная характеристика - нормальное распределение
Частотная характеристика – это график количества штук (например субъектов РФ), для которых какое-то значение попадает в некий диапазон.
Это, например, количество субъектов по процентам городского населения от общей численности за 2012 год:

Здесь есть более-менее явная «вершина» - по 22 субъектам процент между 64.45 и 71.56.
А это – количество легковых автомобилей на 1000 человек по странам мира за 2010 год:
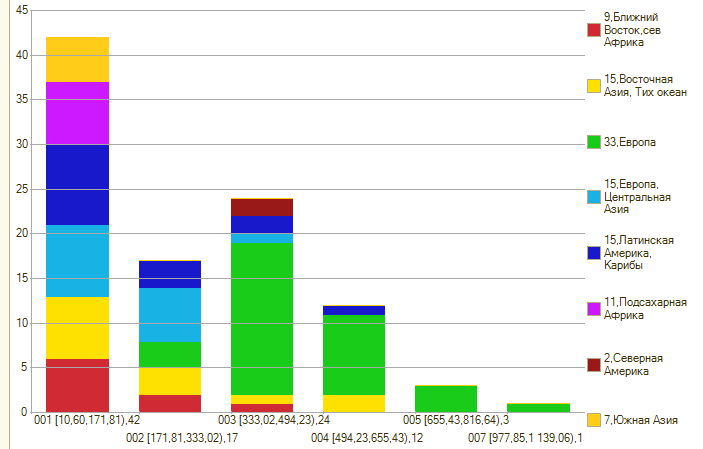
Тут уже две вершины. Обилие автотранспорта в Европе нарушило естественное убывание функции и создало довольно необычную картину частотной характеристики.
Во всех случаях есть какие-то причины, по которым получается так а не иначе. Так выглядит частотное распределение для 10 двухсторонних сбалансированных монеток, которые одновременно подбрасывали 1024 раз:
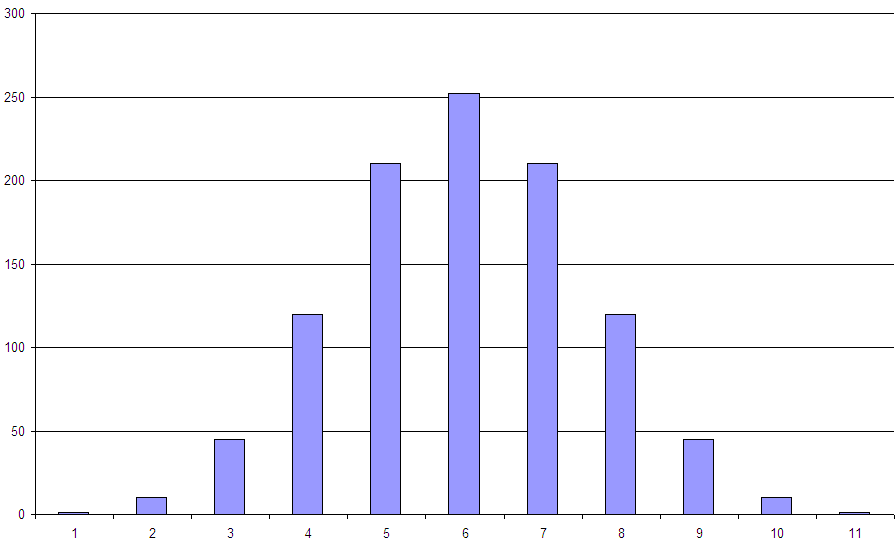
Если частотное распределение похоже на такую одну симметричную гору, то скорее всего частотная характеристика – то самое нормальное распределение (а не какое-то другое, которых много).
Интересно то, что нормальное распределение довольно часто возникает в биологических процессах. Но ведь если результат похож на результат подбрасывания монетки, то можно предположить что в этих биологически процессах действует какая-то сходная внутренняя механика, т.е есть какое-то число факторов, которые либо включились (тогда «1» или решка) или не включились в ситуации (тогда «0» или орёл).
Причём количество факторов явно ограниченно потому что чем больше монеток одновременно подбрасывается, тем меньше дисперсия:
http://akostina76.ucoz.ru/blog/2019-03-21-5728
… что в своё очередь означает, что данные больше прижимаются к среднему значению. Если бы было так, то большее количество экспериментальных данных прижимало бы результат к среднему значению. А реальные данные по биологическим процессам дают более-менее стабильную картину частотной характеристики, для которой можно указать и среднее значение и разброс значений.
Средний срок беременности например 268 дней с отклонением 16. Форма нормального распределения задаётся такой формулой:
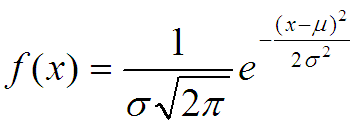
При среднем значении считаемом так:

И стандартном отклонении, считаемом так:
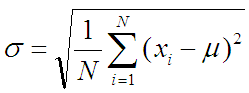
В данном случае ничего считать не надо, потому что экспериментальные данные уже собраны и всё посчитано. И потому общеизвестно, что μ=268 а σ=16.
Можно нарисовать график этого распределения:

Диапазон от 220 до 316 дней выбран не случайно. По картинке видно, что явно почти весь ненулевой график в него попал, что означает что продолжительность беременности меньше 220 дней и больше 316 дней – крайне редкое явление.
Чтобы оценить вероятность продолжительности беременности меньше 220 дней надо проинтегрировать функцию распределения по промежутку от минус бесконечности до 220. Получится так:

Т.е вероятность такого события – одна сотая или 0.1%.
Почти вся единица общей вероятности лежит между 220 и 316 днями:

По функции evalf видно что мне пришлось запустить численный расчёт интеграла, потому что аналитически функция нормального распределения не интегрируется.
В книге есть «жульнический» способ расчёта той же площади – вероятности. По среднему и отклонению можно вычислить значение Z-оценки для любого значения (в данном случае для любого количества дней)

Утверждается что, для основной части информации («горы») это Z болтается в диапазоне от -3 до 3. Если посчитать дни для этих крайних Z, то будет так:
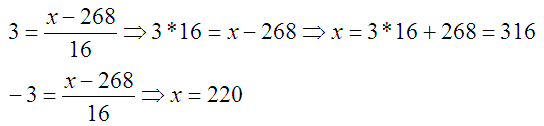
т.е по крайним тройкам Z получается тот самый диапазон дней, в который почти всё попадает.
А чтобы узнать площади вероятность по этому Z существует специальная таблица:
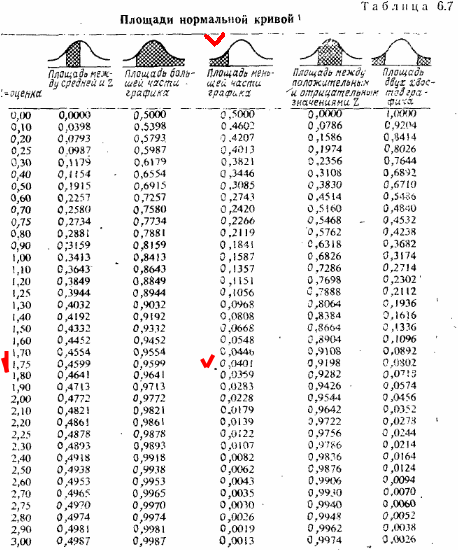
… где каждому Z соответствует та самая площадь.
Если я например хочу узнать вероятность срока 240 дней, я считаю для него Z:

Нахожу нужную строку в таблице и выясняю, что интеграл «хвоста» = 0.0401. Если просто посчитать интеграл по распределению за тот же период, то так и будет:
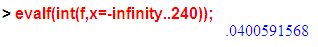
Пример с беременностью, кроме всего прочего интересен довольно большим разбросом значений, т.е стандартное отклонение σ=16. В случае подбрасывания двух монет σ=0.5. При большем количестве монет оно только уменьшается.
Естественно предположить, что факторы в биологических процессах не бинарные, т.е они не только включаются и выключаются (0 или 1) но и могут воздействовать с разной силой. Чтобы увеличить σ можно представить не монетку а игральную кость с 6 возможными вариантами. Её распределение для трёх одновременно брошенных костей:
|
Сумма по трём броскам
|
Комбинаций
|
|
3
|
1
|
|
4
|
3
|
|
5
|
6
|
|
6
|
10
|
|
7
|
15
|
|
8
|
20
|
|
9
|
24
|
|
10
|
26
|
|
11
|
26
|
|
12
|
24
|
|
13
|
20
|
|
14
|
15
|
|
15
|
10
|
|
16
|
6
|
|
17
|
3
|
|
18
|
1
|
Можно представить, что каждый фактор из трёх сильнее и или слабее сдвигает результат вправо (увеличивает). Три единицы (сумма = 3) даёт малое значение (каких-нибудь дней) а три шестёрки (сумма = 18) большое. Дисперсия для такого эксперимента = 8.95.
А вот сколько факторов влияют на срок беременности и сколько у каждого из них возможных результатов не знаю.
Насколько знаю, тут не только генетика влияет (то самое случайное значение конкретных генов) но и внешние условия. Кошек и собак, например, не клонируют потому что окраска определяется не генетикой а условиями формирования плода. Т.е клон любимой кошечки почти наверняка будет иначе выглядеть.
p/s
В физике есть предмет «Физическая механика», в котором собираются вместе известные физические законы (обычно установленные экспериментально) и статистические расчёты, учитывающие, например, хаотическое движение молекул. Двумя разными способами получается один и тот же результат и при этом статистика объясняет эксперимент. Но статистика там не простая, а учитывающая поведение мелких частиц.
В биологии, похоже, наоборот. С помощью эксперимента можно получить статистические данные – закон процесса. Но ведь можно прикинуть и внутреннюю механику, т.е что там включается или выключается, как-то влияя и вызывая такой средний наблюдаемый результат с таким разбросом.
|









