Решение уравнения теплопроводности (1)
Пусть есть уравнение и к нему начальное условие, т.е график температур в начальный момент времени:
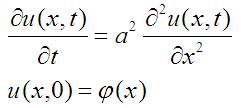
«x» тут координата одномерного «стержня», а «t» - время.
Довольно популярен вариант решения при котором сразу задаются граничные условия, т.е стержень конечен, длина у него L, а на концах температура почему-то равна нулю… не иначе в Кельвинах. Математически посчитать можно что угодно, но я не смогла представить себе этот физический объект. С закреплённой на концах струной всё понятно. Там действительно нулевое смещение. А здесь-то как такое получается?
Привычный метод – поиск решения u(x,t) в виде u(x,t)=X(x)*T(t) в надежде что решение распадается на функцию T(t), зависящую только от времени и функцию X(x) зависящую только от координаты.
Засовываю этот предполагаемый вид в исходное уравнение:

Перетаскиваю всё, что зависит от времени t в одну сторону, а то, что от координаты x – в другую:

Перетащить успешно удалось. А раз между двумя функциями совершенно разных переменных осталось равенство эти соотношения обязаны быть равны какой-то константе λ.
Одно уравнение распалось в систему двух дифференциальных уравнений для X(x) и T(t):

Решением первого уравнения, т.е функции от времени может быть только экспонента, т.е:

Экспоненты бывают возрастающие (при положительном аргументе) и убывающие (при отрицательном):

Не бывает природных процессов при которых температура сама по себе начинает расти да ещё и со скоростью экспоненты. Это означает что λ во всей этой конструкции может быть только отрицательной. Чтобы подчеркнуть этот факт её можно заменить на другую константу: λ=-ω*ω.. Тогда выражение для T(t) имеет вид:

Такая неприятность как интеграл тут возникла потому что ω может быть любым числом. Никаких ограничений на его значения нет. Из-за этого остаётся только просуммировать все возможные варианты. Это и делается с помощью интеграла (который и есть функция суммирования всех вариантов).
Решения дифференциального уравнения относительно X(x) даёт сумму синуса и косинуса и тоже интеграл по всем значениям ω. И это, к сожалению, тупик потому что дальше непонятно что делать. По счастью в хозяйстве имеется начальное условие, позволяющее осуществить замену:

К сожаление интеграл от такой подстановки никуда не делся и при его определённости (от минус бесконечности до плюс бесконечности) осталось непонятно как его преобразовать во что-то более определённое.
Есть инструмент, позволяющий это сделать. Это прямое и обратное преобразование Фурье, которое в данном случае подходит тем, что позволяет выразить функцию через те самые интегралы по аналогичному периоду. Общий вид прямого преобразования:

Здесь появилась такая замечательная штука как мнимая единица «i», т.е произошёл выход из множества обычных – рациональных – вещественных чисел в комплЕксную плоскость.
Обычно считается кто извлечь квадратный корень из отрицательного числа невозможно. Мол нету таких чисел, квадрат которых давал бы отрицательное число. Но извлекать корни очень хотелось. Потому и пришлось придумать тут самую мнимую единицу «i»:

Множество обычных чисел расширяется за счёт комплексной плоскости. Например может быть так:

… т.е некое z равно пяти обычным единицами и трём мнимым.
У этого инструмента (комплексные числа и комплексная плоскость) есть разные применения. Основное известное мне – инструментарий, позволяющий почти автоматически получать картины обтекания воздухом крыльев самолётов различный формы. А здесь эта штука вылезла в виде прямого и обратного преобразования Фурье.
Обратное преобразование выглядит так:

Можно проделать довольно странную, вроде бы, операцию, т.е взять обратное преобразование от прямого чтобы получить вид функции, выраженный через два интеграла от неё же:

В общем виде операция выглядит довольно загадочно, но в данном случае у меня есть вполне конкретной вид функции u(x,t) в которое я именно это и буду засовывать.
Я проведу прямое а потом обратное преобразование функции φ(x), которая у меня заменила X(x). Прямое преобразование:

Единственное, что я изменила в этой записи это букву – аргумент функции. Было «p» а стало «ω». Никто не мешает мне это сделать. А делаю я это потому что подбираюсь к интегралу по этому ω, который у меня возникнет при обратном преобразовании:

Теперь можно это всё засунуть в выражение для u(x,t):

А теперь можно воспользоваться тем, что интегралы можно вынести за «скобки» а потом даже поменять местами:

Внутренний интеграл от ω с кучей экспонент можно сильно упростить, почти вычислить. Для экспонент так:

Потому подынтегральное выражением можно переписать так:

… а дальше заняться прикладным шаманизмом с преобразованием этого выражения. Но это завтра.
|









