Решение уравнения теплопроводности (1)
Пусть есть уравнение и к нему начальное условие, т.е график температур в начальный момент времени:
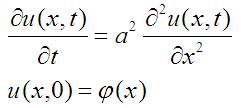
«x» тут координата одномерного «стержня», а «t» - время.
Довольно популярен вариант решения при котором сразу задаются граничные условия, т.е стержень конечен, длина у него L, а на концах температура почему-то равна нулю… не иначе в Кельвинах. Математически посчитать можно что угодно, но я не смогла представить себе этот физический объект. С закреплённой на концах струной всё понятно. Там действительно нулевое смещение. А здесь-то как такое получается?
Привычный метод – поиск решения u(x,t) в виде u(x,t)=X(x)*T(t) в надежде что решение распадается на функцию T(t), зависящую только от времени и функцию X(x) зависящую только от координаты.
Засовываю этот предполагаемый вид в исходн
...
Читать дальше »









