Треугольник Паскаля
Добралась до общепринятого способа решения этой задачи:
http://akostina76.ucoz.ru/blog/2019-03-21-5728
Для 4-х подбрасываний монеты (или 4-х-значного двоичного числа):
https://akostina76.ucoz.ru/blog/2019-03-20-5726
… у меня было нарисовано такое:
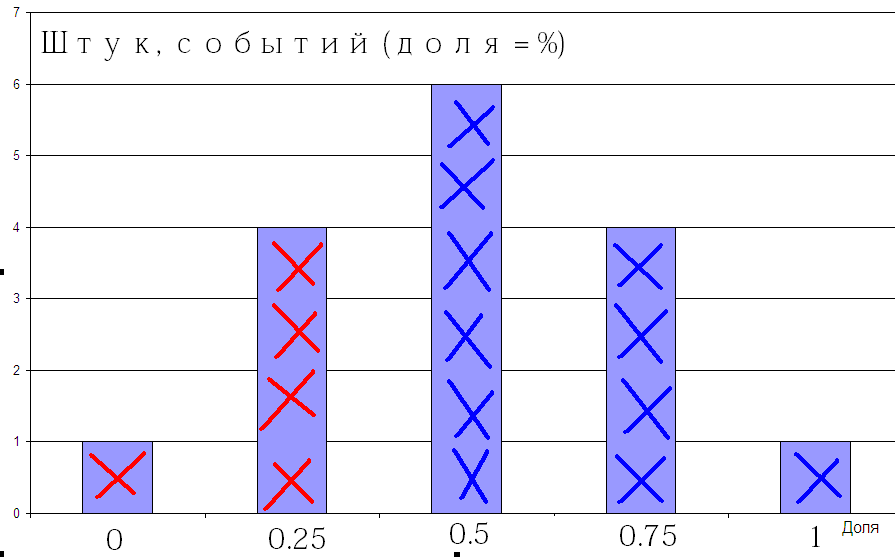
По оси X тут доля нулей (или единиц) в возможном результате. А количество крестиков (ось Y)– количество комбинаций с такой долей.
То же самое (только с количеством) для разного количеств подбрасываний:

Когда так нарисовали, видимо, увидели интересую закономерность в количествах комбинаций. Цифра следующего ряда – сумма цифр слева и справа в предыдущем ряду. А единица с краю – всегда единица, потому что суммируется с нулём.
Два треугольника Паскаля для определения количества комбинаций и вероятностей:

Каждое значение вероятности (нижний треугольник) получается если разделить на два сумму левого и правого значения из предыдущего ряда.
Паскалем надо было быть до такого додуматься))).
Работает:
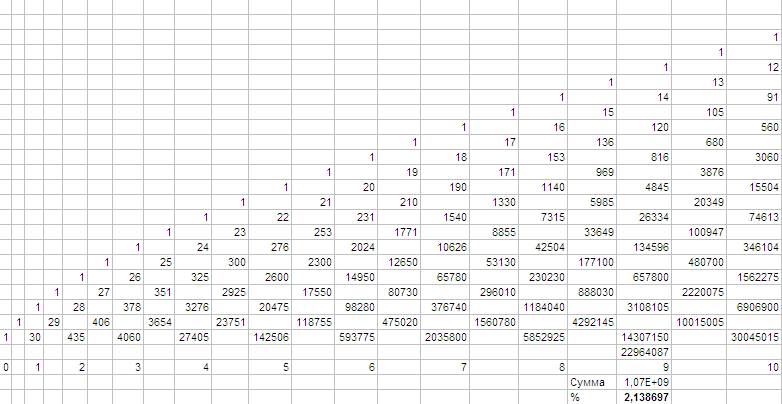
У меня правда получилось, что 9 из 30 будет с вероятностью 2,138697% (в приближённом расчёте получилось 3.58), но, наверное, это не важно.
|









