Расчёт вероятности по t-оценке
Собиралась закончить, но оставлять это всё без понятного расчётного инструмента как-то нехорошо. Данные таблиц излише… дискретны))).
Но вначале про Z-оценку как самый простой пример, хорошо подходящий для графических объяснений.
Пусть у меня есть две выборки. Средние значения (координаты вершины) находятся в точках -1 и 1 (mu1 и mu2):

Разбросы (s1 и s2) подогнаны так (=0.55) чтобы t-оценка была равна 2.57. Это t-оценка для вероятности p= 0.01 при бесконечном N из таблицы, которая тут:
https://akostina76.ucoz.ru/blog/2019-04-13-5779
По значениям средних (mu1 и mu2) и разбросов (s1 и s2) построены два распределения f1 и f2. Но для определения t-оценки используется третье распределение, для которого средняя – одно из средних значений, а разброс – рассчитанное по s1 и s2 значение (s_avg).
Если их всех изобразить на графике то будет так:

Красным тут изображена первая выборка, синим – вторая и чёрным – результирующая, по которой всё считается. От красной (первой) она получила координаты вершины, а шире стала потом что в ней учтены оба разброса.
При расчете считается вероятность получения средней второй выборки (синей) для такого (черного) распределения. А потом она умножается на два (видимо потому, что горка может быть и правее ли левее красного «эталона»).
Вот эти два значения интегралов (площади хвостов чёрной функции f3):
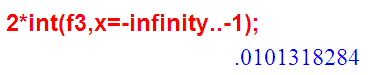
… равны тому самому p=0.01.
t-оценка становится Z-оценкой при N равном бесконечности. При небольших же выборках (которые обычно бывают), интеграл – вероятность надо считать по распределения Стьюдента.
По терминологии. Горка частотного распределения типа такой:

… называется плотностью вероятности и обозначается маленькой буквой f.
Функция же вероятности, нулевая слева, равная единице справа и выглядящая примерно так:
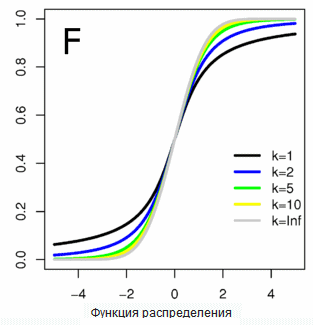
… называется функцией распределения и обозначается большой буквой F. Поскольку F это интеграл от f, то это привычное правило.
Распределение (которое «горка») задаётся такой функцией:
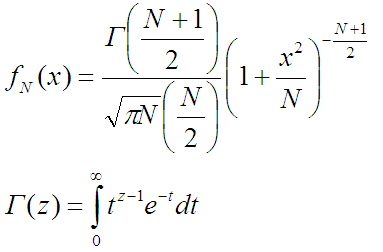
Если затолкать весь этот кошмар в Maple, то он с ним вполне справится:
N:=60;
f_N:=GAMMA((N+1)/2)/ (sqrt(Pi*N) *GAMMA(N/2) ) * (1+x^2/N)^(- (N+1)/2) ;
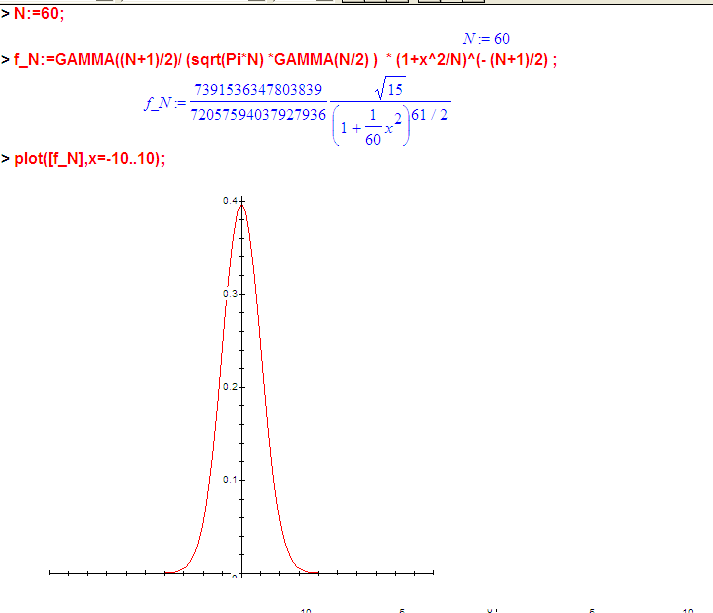
А если по этой функции посчитать площади хвостов (2 * площадь одного хвоста), то будет так:

.. т.е то самое p=0.01 из этой таблицы:
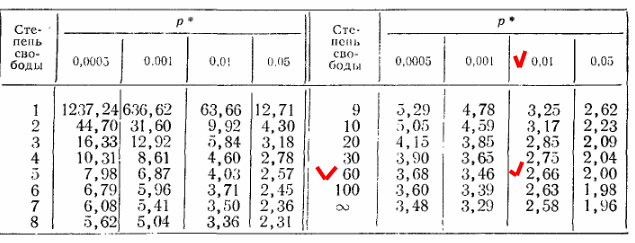
Если интересует 50%-я вероятность (p=0.5) для выборок длиной 3 и 30, то так она так выглядит:

Видно, что с ростом N функция всё ближе прижимается с среднему значению. А поскольку это приводит к тому, что тех самых значений там становится больше, то и интеграл «хвоста» надо считать по чуть большему диапазону, чтобы получить половину вероятности:

|









