Давление и малый объем воздуха

Тут:
https://akostina76.ucoz.ru/blog/2020-07-29-6656

… я не стала разбираться с выводом уравнения для закона сохранения массы, потому что пыталась сформулировать немного другую мысль.
Но вернуться к этому вопросу надо по нескольким причинам.
Во-первых, в следующих уравнениях присутствует давление p. Неплохо бы понять, что это такое не на уровне «интуитивно ясно» (или не ясно?) а чуть лучше. Т.е понять, как этот параметр вплетается во все эти законы и объемы воздуха произвольной и меняющейся формы. В учебнике ни то чтобы вообще не было давления, но там много слов и букв про какие-то тензора каких-то напряжений.
Во-вторых, вроде бы Maple:
https://akostina76.ucoz.ru/publ/7-1-0-97

… решает численно системы дифференциальных уравнений, но не знаю справиться ли с этой. Подозреваю, что в этом случае у меня не хватит энтузиазма на самостоятельное программирование и придётся обойтись общими словами и иллюстрирующими картинками. А для этого надо очень хорошо понимать, что там внутри происходит.
И, наконец, в-третьих. Передача информации в виде готовых уравнений – часть системы, ориентированной на штамповку результатов. Есть уравнения? Всё, быстро ищи тот компьютер, который их решит. Тебе же результат нужен? Всегда и всем нужен результат, но для специалистов каждое уравнение – это слово своеобразного языка. Его смысл, со всеми оттенками известен и так. Без этих пониманий и в компьютер, скорее всего, не удастся задачу засунуть. Это тоже не совсем тривиально.

Для начала – несколько погодных картинок. Вопрос «Что происходит?» возникает ещё раньше, самым первым. Раньше чем придумываются законы и модели с их внутренними абстракциями. Вначале смотрят на происходящее, подмечают закономерности и высказывают хоть какие-то предположения.
Первое – температура:

Всё-таки, в погоде это самое интересное.
Ещё один всегда известный погодный показатель – давление:

… из которого я для экономии места вычла 700 (т.е «36» на экране означает «736»).
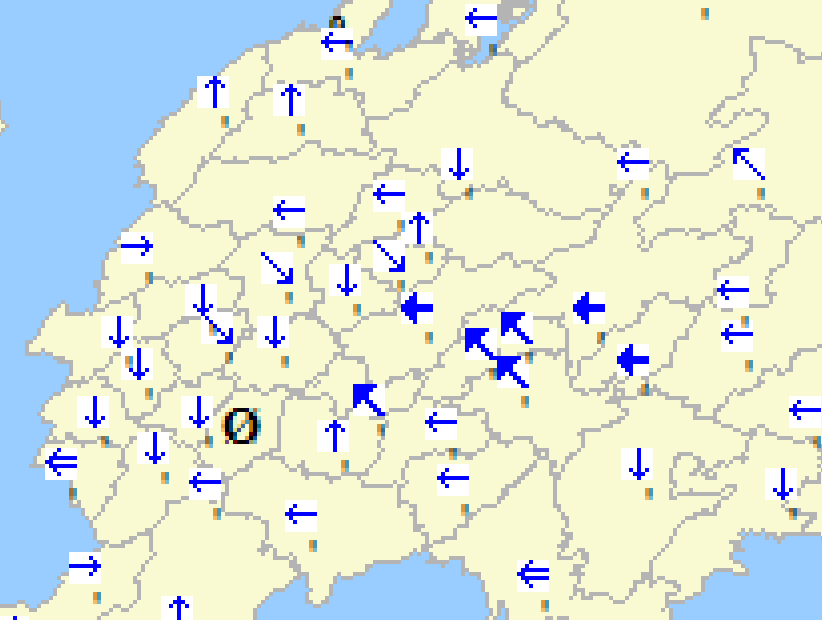
Направление ветра:

Ну и для коллекции - облачность:

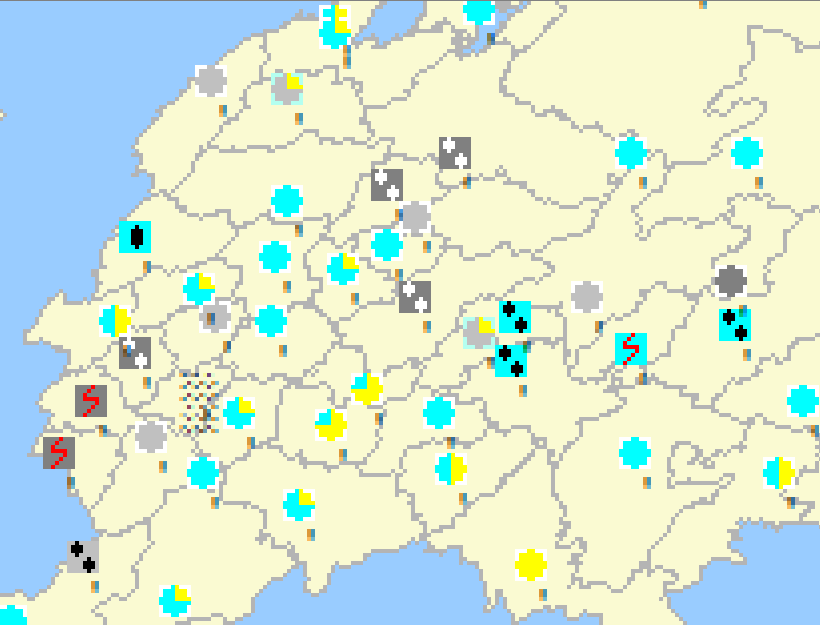
Жёлтый круг – нет облаков, половина голубая – облачность 50%. Не очень уже помню и сейчас не важно. Как тут обозначены дожди и грозы и так понятно. Эти тучи вполне годятся на то, движение чего логично попытаться предугадать.
Буду следить за конкретными тучами, которые были в одной точке этой большой и сложной картинки:
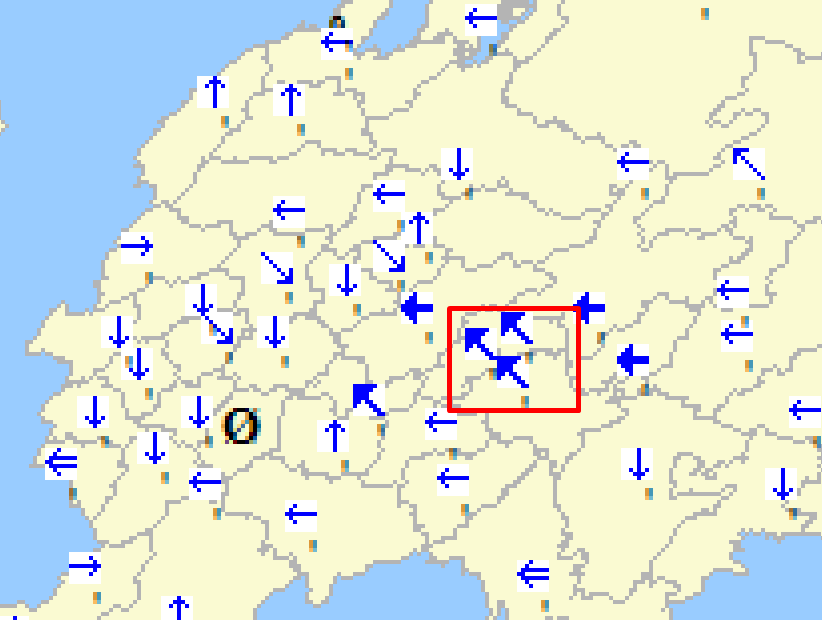
Вот – интересующая туча и ветер, который дует в том районе:
 

Сильному ветру логично сдвинуть тучу влево. Он это и сделал. Через 3 часа было так:

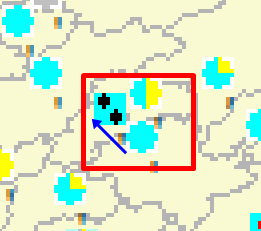
При этом ветром принесло скорее нижнюю тучу. Откуда взялся ветер, т.е перемещение в пространстве молекул воздуха – отдельный вопрос. Но обычно говорят, что тучу принесло ветром.
А теперь вернусь к теории. Сидели люди и смотрели на поведение жидкости или газа примерно так же как я сейчас на картинки.
Тут очень много чего сразу происходит. Естественно выделить из всего этого объема маленький кусочек и посмотреть, что происходит с ним и в нём. Этот кусочек – аналог отдельной тучи, движение которой я попыталась отследить. В масштабах карты это почти точка.
Примерно так и делается:

Вначале я смотрела на весь исследуемый объем воздуха τ, который был над европейской частью России. Я понимаю, что у всего этого воздуха, наверное, масса M какая-то есть…. Ещё он чем-то ограничен, какой-то поверхностью S, на которую со всех сторон дует ветер. Под воздействием всевозможных сил, всё это как-то движется, и, просуммировав все движения молекул, можно получить итоговый вектор количества движения K. Дальше что?
А дальше естественно снизить объем исследуемого, перейдя от наблюдения за всем к наблюдению за точкой или за чем-то к ней близкому. Так хоть что-то увидеть и понять можно. Можно, например, ввести понятие плотности в точке с координатами, стянув пространство в точку, т.е в малый объем:

Раз уж всё пространство заменяется на точку также как и вся атмосфера на отдельную тучу, то можно и другие параметры также определить, скорость этой тучи – точки, например:

Внутри тучи тоже всё движется. Если посмотреть повнимательнее, то можно увидеть что в разные стороны. Абстрагирование со стягиванием объема в бесконечно малую точку позволяет заменить это всё на один, итоговый вектор скорости.
Но скорости и движение не возникает ниоткуда. Чтоб они возникли должна быть приложена какая-то сила.
Чтобы вплести во все это действующую силу, делается нечто довольно странное:

Есть точка, которую можно представить в форме мячика. Понятно, что у неё есть поверхность S. Понято и то, что ко всей этой поверхности S со всех сторон приложены силы, разные по величине и направлениями. Наверное, можно ещё сказать, что нет касательных сил (потому что жидкость, а не твердое тело).  Но давление-то эта точка испытывает со всех сторон. А тут это всё заменяется на приложение какой-то одной силы к части поверхности.
А с другой стороны это логично. Потому что точка – даже не мячик. У неё нет объема, он нулевой. Потому её правая стенка – левая, а нижняя – верхняя. Это, конечно, не так. Но «не так», когда всё стремится к нулю, пренебрежимо мало. А действующие на этот объект силы можно заменить какой-то одной, результирующей.
Осталось добавить, что давление и сила – «родственники». Давление это сила, делённая на площадь. Где больше силы (или давление) оттуда что-то перемещается.
В случае с тучами:

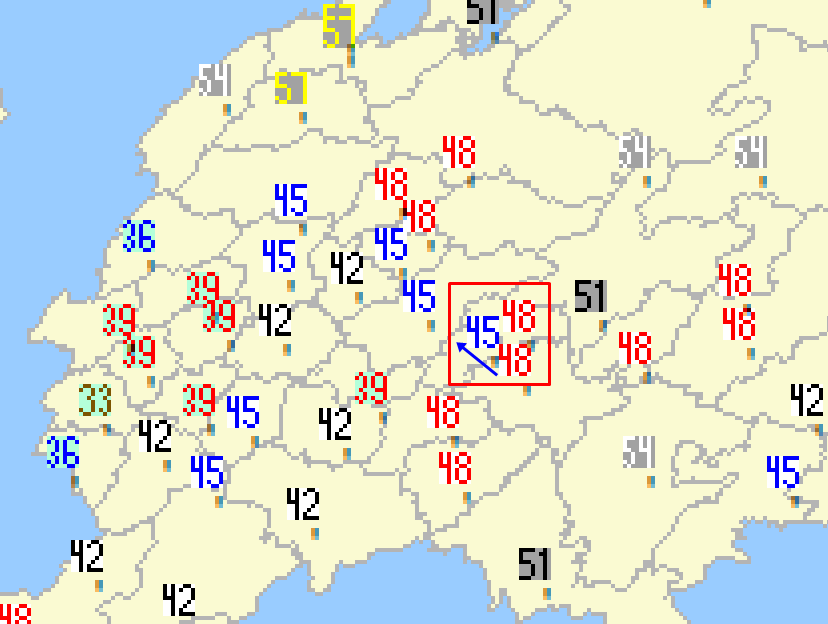
… туча закономерно переместилась туда, где давление было меньше.

Буквой τ, т.е той же, которая на той же странице выше использовалась для обозначения произвольного объема, это, по сути, давление обозначено чтобы враги не разобрались. Шутка. Это просто стандартное обозначение напряжений при описании поведения твёрдых тел (кстати, касательных, а не нормальных), потому здесь они смешались. Букв всех алфавитов меньше, чем всех параметров всех моделей))). Потому так бывает.