Про модель ковида

Любая модель начинается с вопроса «Почему так?». Уже поэтому не бывает настоящих моделей без так или иначе полученных экспериментальных данных. Именно эти данные порождают вопрос «Почему они такие?». Модель это попытка придумать внутренний механизм происходящего, который это происходящее объяснит.
На 29 июля по Москве умерло 4446 а выздоровело 177 908. Это означает, что летальность (процент смертей от суммы) равна 2.44%.
По Петербургу на то же число: смертей 2001, вылечившихся 23199. Летальность – 7.94%.
Почему? Потому что север и бывшее болото. Потому что эпидемии гриппа тут каждый год намного сильнее, чем в Москве, превышают эпидемиологический порог. Место нездоровое. Казалось бы, всё ясно.
Но не всё. Есть ещё такое здоровое места как Дагестан. О здоровье места свидетельствует то, что на Кавказе и близко к нему самая высокая продолжительность жизни. Смертей там 445, а вылечившихся 8174. Летальность – 5.16%. Как они попали к нам компанию по этой летальности?
Если бы всё объяснялось одним ковидом, результат был бы везде одинаковый. Опять вспомню школьный пример про санки, скатывающиеся с горки и проезжающие по земле какое-то расстояние. Пусть везде скатываются одни и те же санки, т.е в эксперименте участвует один и тот же ковид. Если санки проехали после этого разное расстояние, то либо наклон горки разный, либо гладкость горки разная, либо (а почему нет?) в санках что-то ещё лежало в некоторых местах.
Начинаю фантазировать, потому что историй болезни у меня нет, одни смутные предположения. Пусть некто подхватил этот вирус. Сложно мне считать в уме 3%, потому пусть вероятность его смерти 10%. И пусть, если он умрёт, то быстро, т.е через неделю. А если выздоровеет, то процесс растянется на более длительный срок, т.е на месяц.
Смотрю данные по Москве:

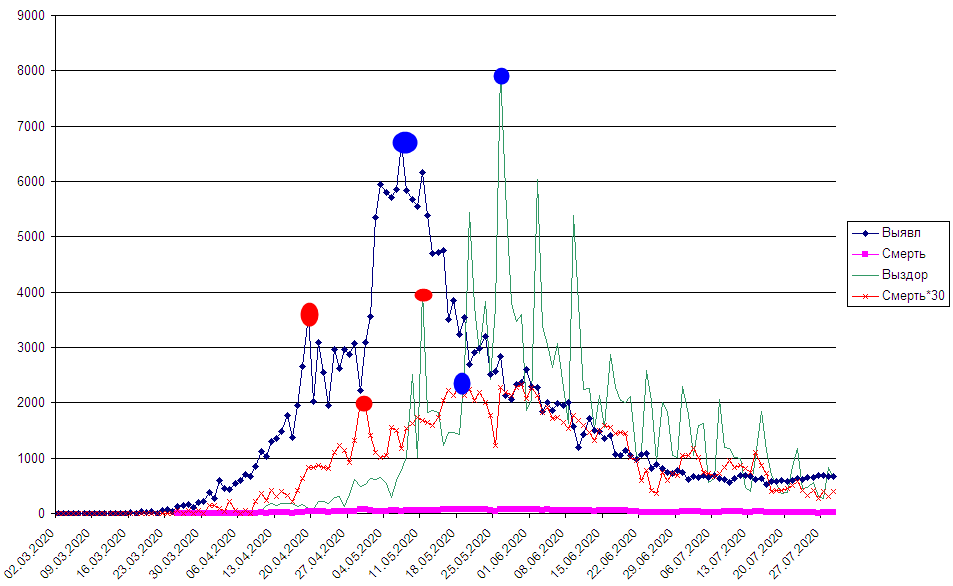
Красный график – количество смертей * 30. Так сделано, чтобы его лучше было видно.
Я вижу, что, действительно, пики смертей и выздоровлений идут вслед за пиками обнаружения этого вируса. Наверное, пора уточнить средние периоды от заражении до смерти или выздоровления по этим данным.
Вот так получается, если просто примерно ткнуть в вершины функций:

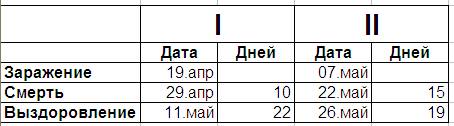
Даже тут вылезает отличие в цифрах, хотя понятно, как получены эти цифры. Если верить цифрам, то со второй вспышки выздоравливают быстрее, а организмы умерших сопротивляются дольше. Что это случайность и погрешность измерения или что-то изменило ситуацию, например, просто убрав самых слабых первыми? Если вспомнить задачу про санки, то можно представить, что санки, съехав первый раз, как-то изменили поверхность горки. Не знаю. Но пока мне проще предположить, что среднее время от заражения до смерти – две недели, а до выздоровлении я- 3 недели.
Я уже прямо сейчас могу сформулировать самую простую модель происходящего, но делать выводы по одному региону – это слишком. Та самая шутка вспоминается «Если по результатам эксперимента надо получить прямую, получайте её по двум точкам» (по двум точкам всегда можно провести прямую, причём единственную). Раз речь идёт про эпидемии, и кто-то утверждает, что смог создать модель эпидемий вообще, то у него не может быть даже данных только по одной эпидемии, должно быть несколько, чем больше тем обоснованнее выводы.  Полученное после расчёта модели должно быть похоже на факт, который был на практике. Данные по Петербургу:

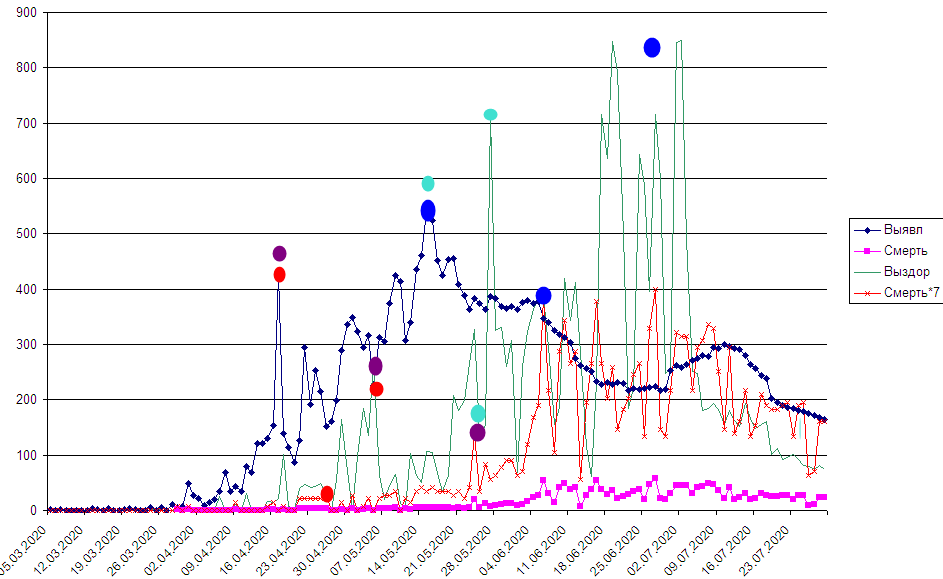
Вот и попробуй разберись, что тут происходит. Т.е уже второй набор экспериментальных данных ни то чтобы разбивает моё предположение, что мрут раньше, а выздоравливают позже и все это через определенных срок (который является свойством вируса) но размывает экспериментальное подтверждение этой гипотезы. По этой картинке можно подобрать как минимум два набора вершин – последовательностей событий:
Так это выглядит:

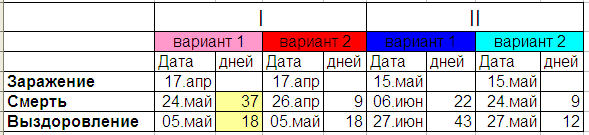
Причём «малиновый» вариант для первой вспышки (если было так, чего я без историй болезней сказать не могу) позволяет сказать, что сопротивляемость настолько различна, и настолько всё от неё зависит, что вряд ли это свойство (параметр модели) можно приписать к вирусу.
Кроме того, картина по Петербургу сложнее. Здесь явно можно говорить а 4-х вспышках заражения.
Не смотря на всю эту неоднозначную экспериментальную информацию, формулирую простейшую модель процесса. Если человек заболел ковидом, он с вероятностью 10% помрёт через неделю или вылечатся через 3 недели. Не точно дата в дату, конечно. Довольно много биологических процессов дают нормальное распределение результатов. Но среднее этих распределений – одна и три недели.
А теперь сама модель:

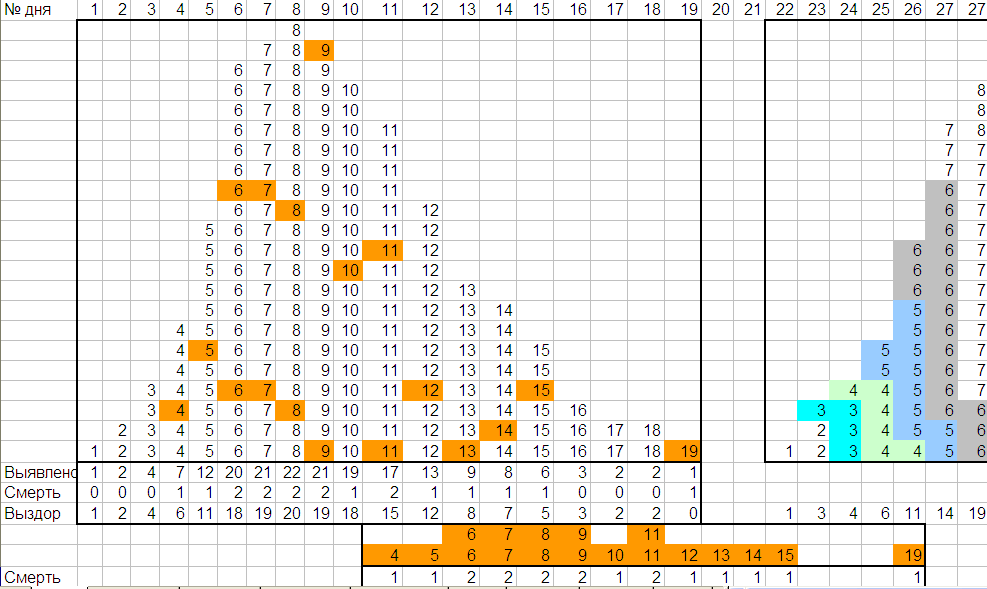
Пусть заражение, не важно чем вызванное, выглядит так, как на картинке слева сверху. Т.е в первый день заболел один человек, во второй 2, в третий – 4. Цифрой указан номер дня, когда этот человек заболел. Заболевший в первый день выздоровеет в 22-й и переместиться на график справа. Смертность по этой модели – 10%. Десятый заболевший появится только на 4-й день (выделено оранжевы). Помрёт он на 11-й день с начала вспышки.
Не все, конечно, умирают и выздоравливают через точное число дней. Там то самое нормальное распределение, у которого есть среднее (координата вершины) и дисперсия (характеризующая разброс, т.е насколько далеко возможные значения разбежались в стороны от вершины).
У меня тут нормальное распределение тоже получилось не совсем нормальное. Я треть выздоровевший раскидывала по соседним дням. Например, выздоровевших в 4-й день было 6 человек. Основная масса (4 человека)  попали в 25-й день и по человеку в 24-й и 26-й. Так собирались суммы выздоровевших за каждый день.
Всё началось с того, что меня удивила и заинтересовала летальность. Для этой модели я её тоже посчитала (в последней строке):

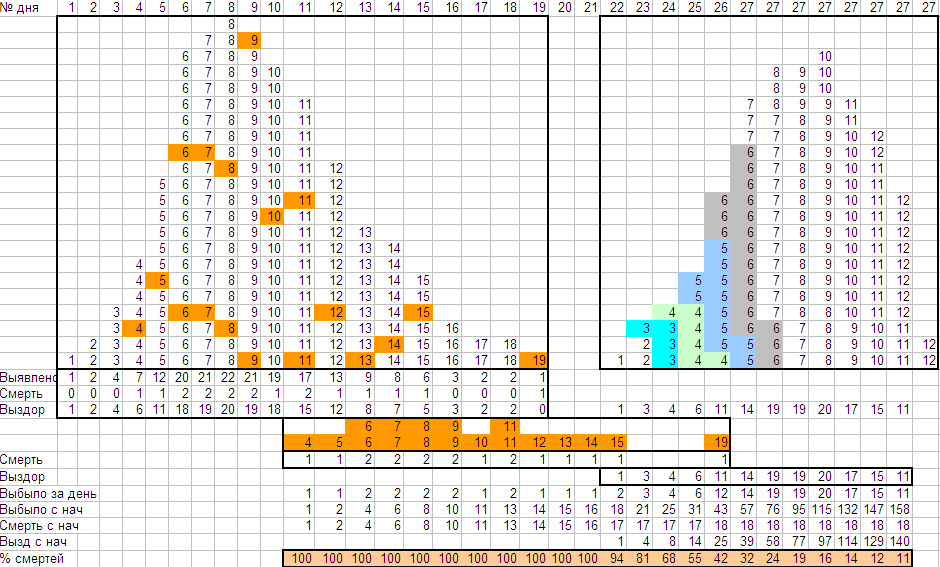
Её график выглядит так:

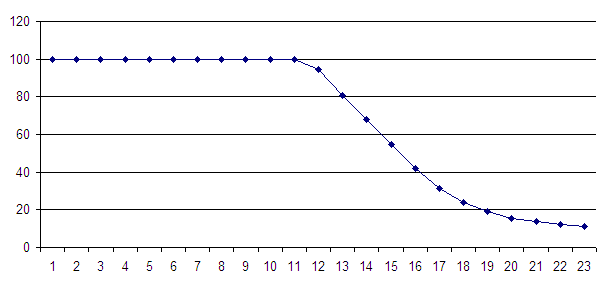
При всей несерьезности того. что выше, даже это позволяет сказать, что модель позволила получить поведение, сходное с реальным.
Вот, например, данные по Италии где, так понимаю, всё уже закончилось:
https://www.worldometers.info/coronavirus/country/italy/

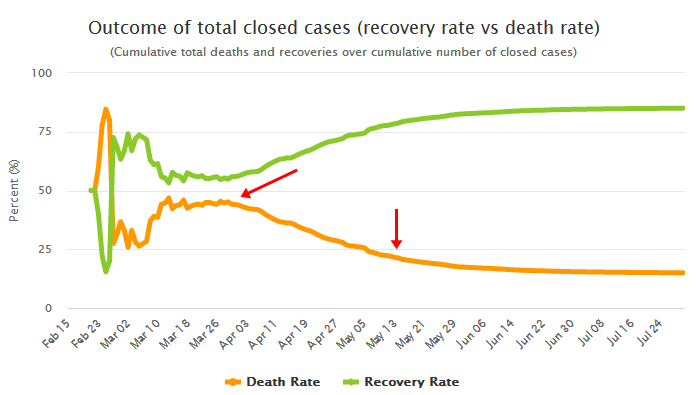
Реальные данные это тоже убывающая функция с двумя точками перегибов. Более сложная форма реальных данных может объясняться несколькими вспышками. А начальный рост функции (а не 100% смертность довольно долго) легко можно получить поиграв параметрами модели. В этой модели уже 4 параметра. Два средних времени (от заражения до смерти и от заражения до выздоровления) и два разброса (опять же по смерти и выздоровлению). Увеличив разброс выздоровлении легко сделать так, что уже кто-то успеет выздороветь когда появятся первые умершие.

При этом, если нет объяснения, откуда взялась эту цифра, это будут во многом подгонка под реальность. С другой стороны, даже такая информация, которая просто есть без объяснений, может быть интересна. В своё время людей у метро ловили и измеряли давление. А как ещё поймать этого среднего человека, который предпочитает не обращаться в поликлиники и узнать, что с ним твориться? Для всех заболевших есть дата обнаружения ковида и выздоровления или смерти. Значит для всех регионов можно вытащить не потолочные значения среднего времени до смерти и выздоровления до смертей а реальные. Ковид везде затронул довольно большие группы населения. Насколько репрезентативна эта выборка – вопрос сложный. Но и это выборка, которая дала реальную информацию. По ней можно делать какие-то выводы о состоянии здоровья среднего человека в каком-то регионе. По ней можно делать выводы о том, как вообще протекают такие процессы. Есть там то самое увеличение срока до смерти и уменьшение срока до выздоровления со временем или нет?  По-моему, интересно дополнить этими данными прочую информацию о состоянии здоровья населения. Ещё интереснее – попытаться это как-то объяснить.
Интересно, всё-таки сравнить летальность. А для этого надо ещё понять как их сравнивать. Буду считать первым днём день, когда умирать начали каждый день. В Москве это 31 марта, в Петербурге – 21 апреля. В Дагестане – 15 апреля.
Так у меня получилось (по X – дней от начальной даты для региона):

Вид, похожий на модель, получился только для Москвы. В остальных местах всё как-то иначе происходит. Никто не хочет попытаться понять почему? Тут должно быть какое-то усложнение модели.
p/s
По виду то, что происходит в Петербурге чем-то похоже на пластичность. Нагрузки меньше предела упругости не вызывают необратимых деформаций. Если их убрать, то всё возвращается в исходное состояние. Здесь же в районе 41-го и 73-го дня какое-то воздействие направляет график в сторону ухудшения. Это 1 июня и 3 июля:

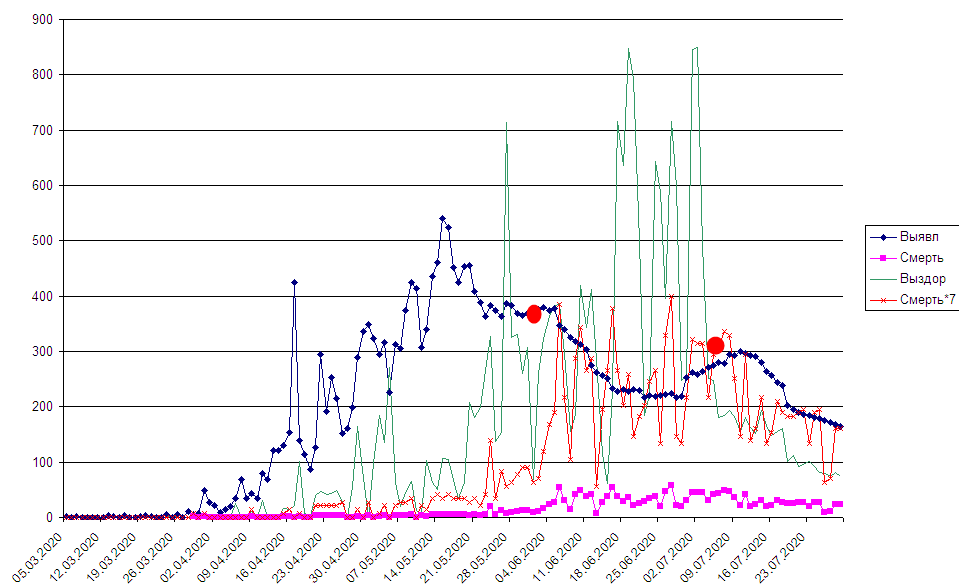
В эти моменты происходят не только вспышки заражения, но и резкое изменение соотношения умерших и выздоровевших. Может эти вещи как-то связаны? Т.е есть некое общее усилие, прикалываемое к иммунной системе людей, которое и заражение упрощает, и ход болезни утяжеляет? И его приложение в какой-то момент приводит к этой то ли «пластичности», то ли разрушению  (разрушение это когда деформации продолжают расти без увеличения нагрузки)? Т.е в данном случае либо к увеличению смертей, либо к увеличению срока болезни.