Формула плоскости и матрицы
Вчера online-сервис вернул мне формулу плоскости по трём точкам:
https://akostina76.ucoz.ru/blog/2020-08-25-6697
… в стандартном виде. Но этот вид, мало того что неинтуитивный, потому что давление вместе с координатами попало в левую часть уравнения, так ещё и неудобный. Мне потом пришлось ещё выковыривать этот Z чтобы получить его значение.
Потому я решила сама посчитать эту формулу плоскости. Для этого мне потребуется такое понятие как «матрица». Оно описывается в одном из математических предметов – в алгебре.
Но всё по порядку. Формулу плоскости хочу в таком виде:
P=a*x+b*y+c
Параметры a,b и с мне не известны. Я хочу их узнать. Чтобы узнать значения какого-то количества неизвестных обычно требуется столько же уравнений. У меня три неизвестных и я могу написать формулу плоскости для трёх известных точек, по которым она будут определяться:

У меня тут немного неинтуитивно то, что наборы x и y известны, а то, что обычно обозначает известные параметры (a,b,c) необходимо найти. Но с другими буквами было бы ещё хуже, по –моему.
Суть в том, что от простейшего уравнения
α*X=β
… где α и β известные цифры, а найти требуется неизвестную цифру X, написанное выше отличается количеством букв, но не задачей. Просто выше при решении этих уравнении надо найти не одну цифру, а три.
Ответ должен быть как-то так записан:
X={a,b,c}.
Но ведь если продолжать аналогию с самым простым уравнением, то видно что и правая часть (т.е β) это тоже три цифры. Т.е:
β={750.2, 748.8, 749.8}
Осталось разобраться с α, которая тут представлена аж 9-ю цифрами. Это не сложно. Всё вместе можно записать и так:
 . .
То, что квадратное (т.е α) в местной терминологии называется матрицей. А трёзцифровое (т.е X и β) называется векторами. Чаще всего цифр именно три. Довольно часто они означают координаты в трёхмерном пространстве. Но может быть и сколько угодно. И размер матрицы будет соответствовать размеру векторов.
Осталось только добавить, что вместо маленьких греческих букв для обозначения матриц и векторов обычно используют большие латинские:
A*X=B
Можно, наверное, сказать, что простейшее уравнение a*x=b – частный случай для одномерного пространства.
То, что мне надо решить для получения формулы плоскости называется системой линейных уравнений. Система потому что уравнений больше чем одно. А линейные уравнения потому, что в них нет даже квадратов (x*x) способных искривить прямую линию функции.
Решать эту систему руками я, конечно, не буду. Так далеко в математику я уходить не хочу)).
Сюда эту систему можно засунуть:
http://matematikam.ru/solve-equations/sistema-gaus.php

… и всё само не только посчитается, но и нарисуется со всеми расчётными этапами:


Вручную такое и подобное считают студенты первого курса один раз в жизни. Причём считают сразу всей группой. Если хотя бы у двоих ответы совпадут, то это, скорее всего – правильный ответ.
Полученное – это и есть искомые a,b,c.
Можно подставить в формулу для плоскости координаты точки, откуда прилетел в Иваново воздух:
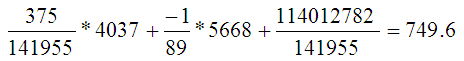
… и получить точно такое же значение давления.
Ответ получен, но раз уж зашла речь об алгебре, то кое-что добавлю. Самое смешное, что от неё остаётся это выражение «транспонировать свою матрицу».
Про что там, я тоже, естественно, уже не помню. Но весь инструментарий, позволяющий работать с матрицами и векторами, описывается явно именно там.
Например, при решении такого уравнения:
2*x=6
… ответ можно получить, умножив всё на число, обратное двойке. Обратная величина эта такая, при умножении на которую получается 1.
Обратное для 2 – 1 / 2. Потому что 1/ 2* 2 =1.
А если умножить на 1 / 2 правую часть уравнения, то получится ответ: 6* 1.2 = 3.
У матриц, как и у чисел, тоже есть обратные матрицы, только при умножении их друг на друга получается матрица с единицами по диагонали и с нулями в других местах:
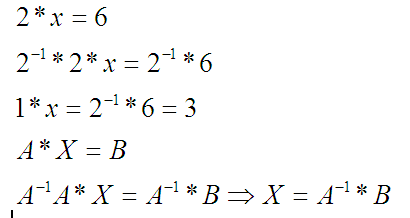
Обратную матрицу я тоже, конечно, руками считать не буду:
http://matematikam.ru/matrici-online/inverse.php

А сразу возьму ответ:
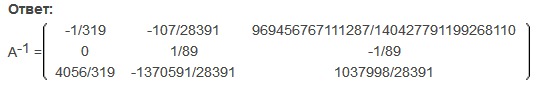
Как матрица умножается на вектор видно по системе уравнений. Строки матрицы последовательно умножаются на один и тот же столбец:
 .. ..
То же самое можно записать тремя строками уравнений.
А матрицы перемножаются так:

Результат – тоже матрица из 9 (в данном случае) цифр.
Кому не лень, может убедиться, что умножение обратной матрицы на исходную даст такое:

… а умножение обратной матрицы на столбец – вектор давлений даст параметры формулы плоскости.
p/s
А транспонированная матрица это та, у которой цифры на диагонали такие же, а всё остальное зеркально отразилось от диагонали. Т.е то, что было справа сверху, стало слева снизу (и наоборот).
|









