Балансировка и оптимальные габариты ракеты

Самое время кое-что посчитать. Имеется ракета, центр тяжести которой там где молоток:

И у левой и у правой половины есть более-менее известные массы, но приравнивать их бессмысленно потому что действуют не они (точечные), приложенные в некой точке, а суммарный момент M=F*L, т.е сила тяжести умноженная на плечо (плечо -  расстояние от молотка до места нахождения давящей массы).
И тут всё довольно неприятно потому что не точечные массы, а довольно длинные гильза и хвост. При такой форме надо учитывать то самое плечо, т.е расстояние «ломтика колбасы» от молотка (потому что чем больше расстояние тем «тяжелее» давит «ломтик»). И все эти моменты (M=F*L) надо просуммировать.
Для суммирования (в дано случае по длине) используются интегралы, та самая вытянутая буква S, означающая «сумма»:

Буквой ρ тут обозначена погонная масса. Надо же было её как-то обозначить. Деревяшка длиной 151 см весила 49 грамм. Значит это самое ρ для деревяшки = 49 грамм / 151 см = 0.325 гр/см.
Интеграл для давящего момента правой части (хвоста):

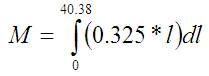
Функция под интегралом очень простая, потому можно сказать, что интеграл вычисляется по стандартной формуле из таблицы, вот такой:

С левой частью сложнее потому что она составная. Там есть и деревяшка и гильза ( на некотором расстоянии от молотка и порох, который от молотка ещё дальше.
15 сантиметров гильзы весят 12 грамм, т.е плотность = 12/15=0/8.
Порох передней части – 12 см весит 13 грамм, т.е плотность = 1.08
Осталось всё это аккуратно засунуть в интегралы и просуммировать:

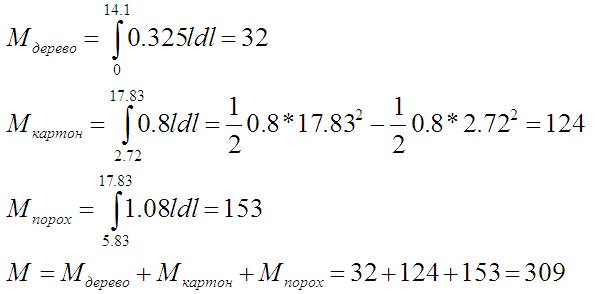
309 слева существенно больше чем 265 справа… Теоретически должно быть равно. Другое дело что точность взвешивания… не идеальна.
Чем длиннее хвост тем легче ракета, которую должна поднимать тяга. Вес можно снизить за счёт длины. Хвост вдвое большей длины (81 см) и погонной массой 0.09 (т.е в 3 с лишним раза тоньше) весил бы вдвое меньше и балансировал бы ракету точно также.
Вес можно снизить и за счёт формы самой ракеты. Ведь гильза довольно тяжёлая и её тоже приходится поднимать. Интересно каким должно быть соотношение радиуса и длины чтобы площадь стенок (т.е масса гильзы) была как можно меньше а количество засунутого в гильзу горючего (т.е внутренний объем) как можно больше.
Вот такая штука:

Хочу чтобы площадь поверхностей S была минимальная:

Вот такая функция получилась. Остаётся надеяться что минимум у неё есть. И он там есть:

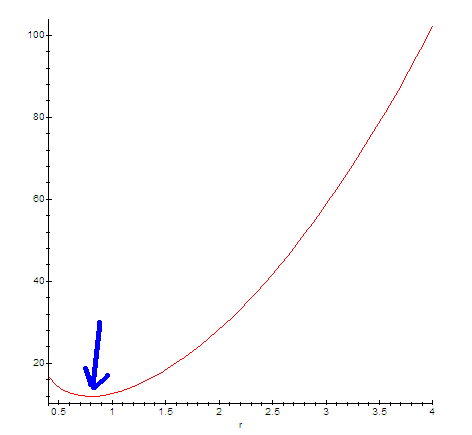
Неплохо бы ещё точно узнать, где находится эта точка. А находится она там, где первая производная равна нулю. Действительно, приращение по горизонтальной оси X в этой точке никуда не девается, функция благополучно сдвигается вправо. А вот изменения горизонтального Y в таких «горбах» нету. А производная (по определению) это приращение Y делённое на приращение X.
Считать даже такую примитивную производную руками мне лень. Вот она:

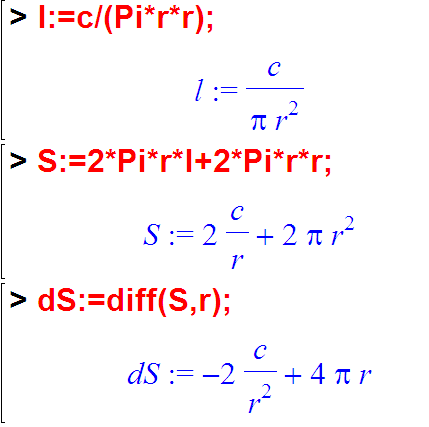
… (выражение dS).
Осталось задаться каким-то значением константы C и приравнять dS к нулю. Потом это уравнение надо решить, т.е найти R. Пусть константа C=ПИ=3/14. Тогда так:
R=1/2*2^(2/3)=0.79.
График функции S (красный) и её производной (синий):

… проходящей через ноль в той самой точке минимума.
А диаметр, т.е два радиуса = 1.587. И то же значение для высоты цилиндра L, если в неё подставить радиус.
Это означает, что минимальный вес у гильзы будет когда гильза будет похожа на кубик или круглый шарик (длина равна диаметру). Первый спутник был тем самым шариком с длинными ножками.