Дробные числа
Компьютеру сложно и неудобно работать с дробными числами. Это для него непонятая реальность. Ведь в компьютере внутри есть нули и единицы, означающие, по сути, есть электрический ток или нет. Группы битов (т.е 0 и 1) можно объединить в байты с помощью которых легко хранить целые числа и что-то с ними делать.
А число с дробью, т.е число с плавающей точкой (float) это для начала непонятно что. С какой точностью его хранить-то? И как, по каким правилам, с ним дальше работать особенно учитывая то, что и арифметика серьёзно усложняешься, т.к. точность (количество знаков после запятой) превращает 1+2=? в работу с миллионами (если 6 знаков после запятой). Просто только в теории. Ведь от процессоров требуется быстродействие а не просто как-нибудь посчитать.
Я точно не помню и не особо этим интересовалась. Но было бы странно если бы в компьютере, изначально предназначенном для вычисления, на аппаратном (т.е железном) уровне не было бы что-то придумано специально для выполнения этих изначально «тяжелых» операция с дробными числами. Его и придумали. В процессорах есть какой-то блок (т.е нечто спаянное, а не программное) который занимается операциями с такими числами. Микросхемы работают намного быстрее программ и выдают какой-то результат. Единственный недостаток – что-то спаянное уже никак невозможно поменять. Вот и этот кусок процессора, который выполняет операции с дробями что-то получает и что-то возвращает.
Но есть небольшая проблема. Он может сохранить число = 1 как 0.99999999. Множество девяток это тоже единица. А разве нет? Но если сравнить её с той единицей которую он почему-то сохранил как 1.00000001, то он правильно сообщит, что это разные цифры.
Если я напишу:
float a,b;
a=1; b=1;
if(a==b) {
printf(“Равно”,%s);
}
… в надежде, что оно сообщит о равенстве, то это может и не сработать.
Древнее (и до сих пор работающее в подобных случаях) решение проблемы – использование функции abs(), т.е модуль числа. Модуль числа равен числу если число положительное и минус числу, если число отрицательное.
А примере выше надо писать
if(abs(a-b)<0.01) {
printf(“Равно”,%s);
}
Пример был на языке Турбо Си. И можно говорить о том, что компилятор Турбо Си был немного несовершенен раз требовал такого написания. Объяснение, что так работает «железная» часть компьютера не очень убедительное. Ведь компилятор это программная надстройка над этой железной частью и она достаточно гибкая чтобы исправить ситуацию на своём уровне.
И ситуацию исправили. Если не ошибаюсь, уже в Borland C++ кроме float (с проблемой) появился тип double (точно такой же но без этой проблемы). float был оставлен для совместимости языков. У других языков нет столь долгой истории потому в них с самого начала не было такой проблемы.
Но ведь float нужен не так уж и часто. Намного чаще приходится работать с целыми числами. А целые числа это нечто родное для машины. С ними никаких проблем. Достаточно написать, что они целые (int) и такое прекрасно сработает:
int a,b;
a=1; b=1;
if(a==b) {
printf(“Равно”,%s);
}
Т.е я отгораживаюсь от проблемы четким заданием типа переменной (float, int) и случайно встретиться с ней не могу.
Но в последнее время программист пошёл ленивый. К тому же машинные мощности позволяют отказаться от обязательного описания переменных. Тип определяется в момент присвоения и даже меняться может если присвоить что-то другое. Современные машины гоняют байты по памяти со скоростью достаточной чтобы выполнять эти неоднозначные по быстродействию операции. Появился тип Variant означающий «что угодно». Но если уж программисту даются такие возможности довольно странно если из какого-то компилятора или интерпретатора полезет древняя, массово решённая в 1995 году проблема. Но теоретически может. На аппаратном уровне всё могло остаться по-старому и если программный уровень как-то криво написан может вылезти и это.
Вторая возможная причина. Данные в базе тоже могут храниться в виде чисел с плавающий точкой Цены с копейками, например, так храниться:
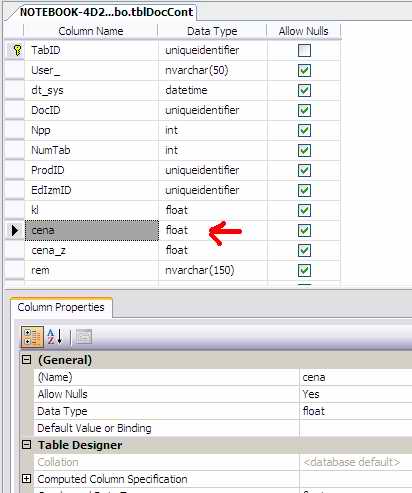
… и нет возможности задать точность этому типу float.
А данные в ней запросто могут записаться вот такие:
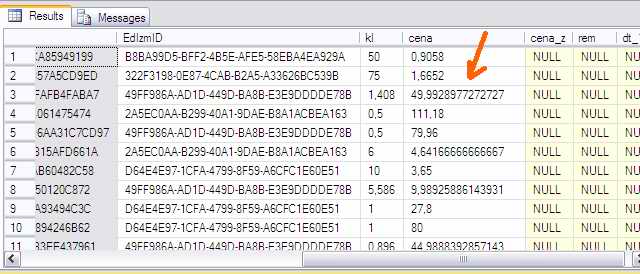
… потому что очень часто цена считается как сумма по строке, делённая на количество.
Если перемножить цену и количество, но нигде не будет этих цифр с «бахромой»:
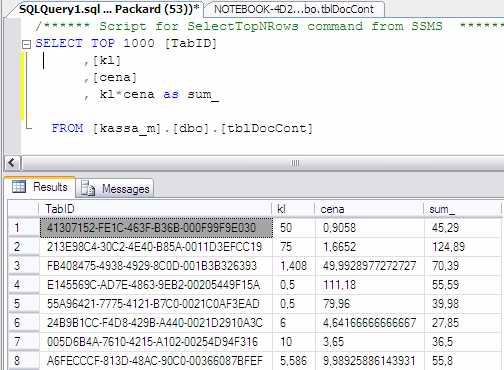
Везде будут нормальные копейки.
При работе с копейками и округлениями есть сложности что называется на идеологическом уровне. Как-то пытаются это всё записывать и хранить так чтобы эти погрешности при округлении поменьше вылезали. Что-то получается, как-то храниться. Но внутри может присутствовать вся эта бахрома, которую пользователь через программу обычно не видит. Ведь в программе пытаются показывать информацию так, как это удобно. Смотреть на это 9 в периоде неудобно. К тому же это занимает место на экране, которое обычно не бывает лишним. Потому для экранного представления информации обычно используются форматы. При таком формате:

… на экране будет показано только три цифры после запятой, хотя реально может быть намного больше.
С проблемой сравнения при таком хранении информации борются с помощью все того же сравнения через ABS: if(abs(a-b))<0.01.
Если не ошибаюсь, у 1С нет такой проблемы. Во всяком случае один молодой человек был очень удивлён увидев моё привычное abs() из-за опасения что если написать общепринятым способом случится что-нибудь страшное. Видимо, там этой проблемы не было. Дело в том, что 1С это надстройка над базой. Видимо пропуская информацию через себя система её чистит от таких вещей, округляя до заданной точности:

.. и так было с самого начала.
|









