Движение Земли вокруг Солнца…или наоборот
Астрономия оказалась очень поучительным предметом. Реальность, данная в ощущениях вовсе не обязана быть реальностью. Шуточная фраза «Хватай мешки, вокзал отходит» как раз про это. Глаза не дадут ответа на вопрос, что движется. Тоже самое и с вращением Земли и Солнца. Два принципиально разных процесса могут выглядеть одинаково.
Интересным мне показалось то, что в расчёте можно сохранить ошибочную, в каком-то смысле модель. Но результат всё равно будет правильным.
Перед тем как считать, надо нарисовать. Земля вращается вокруг Солнца и возникает блин… в хорошем смысле этого слова, т.е некая двухмерная задача потому что всё происходит в плоскости траектории Земли.
Принципиальная схема происходящего это то, что тут:

… нарисовано черной линией. Это круги, потому что всё происходит в плоскости. Это вращение маленького круга вокруг большого. Уже тут, на самом деле все некорректно, потому что нет никаких кругов. Есть точки.
Диаметр Солнца = 1 392 700 км
Диаметр Земли – 12 742 км
Расстояние от Солнца до Земли – 147 098 291 км.
Если я возьму за единицу миллион километров, то Солнце станет точкой с диаметром 1, а Земля будет невидимой точкой в 150 таких диаметрах от него.
Синим, красным и малиновым пририсованы уже мои «фантазии».
Обычно в плоскости используют прямоугольную систему координат, в которой положение точки задаются координатами X, Y. Но иногда, как в данном случае, удобно использовать так называемую полярную систему координат:
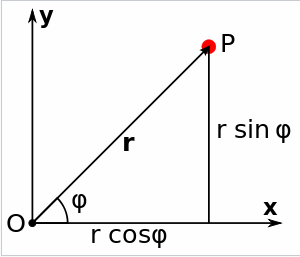
… к которой положение точки задаётся расстоянием до неё и углом от нулевого положения. Нулевое положение это строго направо. Углы отматываются против часовой стрелки. Полный круг это либо 2*ПИ либо 360 градусов. А раз уж речь об астрономии, то это и 24 часа, за которые прокручивается Земля.
На картинках с вращением Земли у меня на всех этих Землях, т.е на положениях Земли весной, летом, осенью и зимой нарисована та самая полярная система координат.
Тут все – мой личный произвол. Захотелось мне чтобы весной угол был нулевым – нарисовала а «весеннюю» Землю левее Солнца. Нету во вселенной никаких координат, потому могу направить любые оси куда угодно.
Да и выбор нуля, т.е точки начала системы координат у меня находится в центре Земли. Логичнее было бы поместить его в центр Солнца и получить, кстати, все то же вращение против часовой стрелки. Только при таком выборе естественно было бы поместить весеннюю землю справа на картинке. Тогда весной был бы тот же естественный ноль градусов.
Но нарисовано как нарисовано, потому что я сижу на Земле и мне так удобнее.
Раз уж я сижу на Земле, то, вроде бы странно помещать начало координат в центр Земли. Но я так делаю, потому что расстояние от Земли до Солнца делает круги точками. Корректнее вообще стереть эти круги и оставить оси системы координат, т.е какие-то направления осей и векторов.
Меня пока интересует угол направления с Земли на Солнце в любой день (это называется долгота). В четырёх точках понятно. В остальных, вообще-то, можно посчитать, используя элементарную арифметику, т.е взяв приращение угла за день как 365 дней / 360 градусов.
Но, всё-таки, лучше взять формулы отсюда:
http://stjarnhimlen.se/comp/tutorial.html
… так будет точнее.
Погрешности вычисления начинают вылезать на больших временных интервалах, потому астрономы вынуждены учитывать реальные особенности вращения тел, а не модели типа «Земля движется вокруг Солнца по кругу»
Во-первых, там не круг, а эллипс:
https://ru.wikipedia.org/wiki/Эллипс
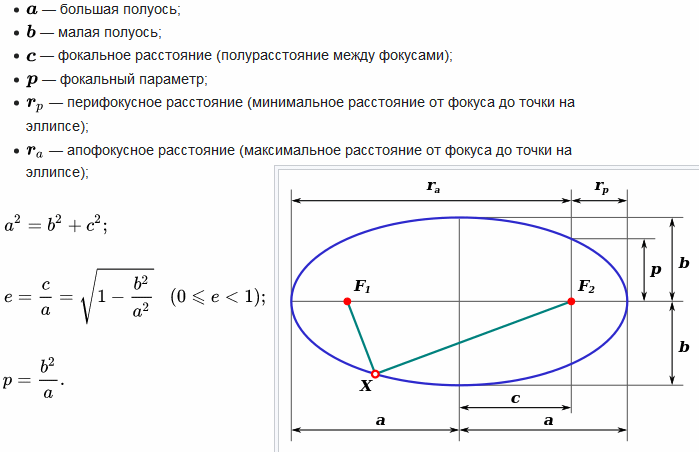
У круга есть радиус r, а у эллипса… два радиуса длинный и короткий (a и b).
По этим величинам можно посчитать эксцентриситет е, который для орбиты Земли примерно 0.017. У круга его тоже можно посчитать, у него ноль.
Орбита Земли очень похожа на круг. Если взять a этого эллипса равным 1, то b=0.99986. Если в расчёте считать эллипс кругом, то точность вычисления пострадает на 1 градус за 20 лет. Учитывать или нет – вопрос вкуса и целей использования.
Во-вторых, вращающийся эллипс постепенно поворачивается в плоскости вращения:

… правда за год он разворачивается на 0.2 градуса, т.е тоже очень немного.
Дальше придётся ввернуть в текст новое слово. Перигелий – минимальное расстояние от Солнца до Земли:
https://ru.wikipedia.org/wiki/Перигелий
На этой картинке:
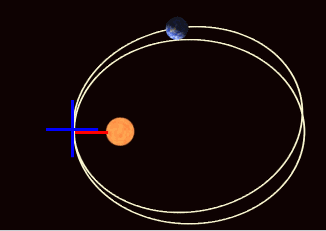
… перигелий будет весной. А его долгота при выбранной системе координат с центром на Земле будет порядка нуля градусов.
Судя по всему, у астрономов есть таблицы, в которых зафиксирована точная информация в какой-то момент. Конкретно в тексте по ссылке в качестве базовых используются данные на 1 января 2000 года. Уже от этой даты всё отматывается с приемлемой точностью на сто лет вперёд или назад.
Номер дня, в который надо узнать положение Солнца относительно Земли считается по такой формуле:
d = 367 * Y - (7 * (Y + ((M + 9) / 12))) / 4 + (275 * M) / 9 + D – 730530
При всей загадочности формулы, она прибавляет 1 день к каждой следующей дате (я проверяла).
Долгота перигелия в день d считается по такой формуле:
w=282,9404 + 0,0000470935 * d
Почему эта величина обозвана средней аномалией я не знаю:
M=356,047 + 0,9856002585 * d
… зато 0.98 это почти 1 градус поворота за день. Попросту говоря в этом М и считается, насколько всё повернулось от базового значения за заданное количество дней.
Скорее всего, градусов M получится очень много (лишних кругов столько сколько лет от базовой даты). Чтобы было похоже на градусы нужно вычесть столько кругов по 360 градусов, сколько их там лишних. Чтобы получить долготу положения Солнца относительно Земли L надо прибавить к остатку М значение w.
Можно ещё учесть эллиптическую орбиту. Это и делается в тексте по ссылке. Тогда будет ещё точнее.
|









