Конформное отображение

В математике есть понятие конформного отображения. Смысл примерно такой. Есть функция, например парабола, т.е y = x*x. Выглядит она так:
http://matematikam.ru/calculate-online/grafik.php

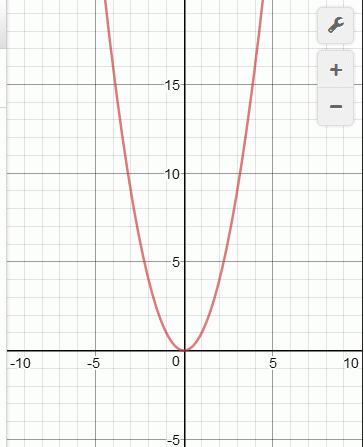
А теперь я возьму синус от этой функции, т.е y = sin(x*x):

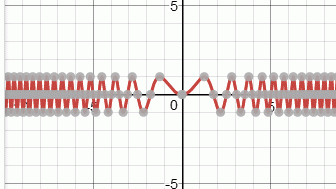
По внешнему виду даже близко не похоже. Но синус был применён как функция преобразования именно к параболе.
Любая функция это набор мест точек. На плоскости с параболой из всех точек двухмерной плоскости в функцию входит только малая их часть. Тоже самое и со второй функцией. Но всем точкам исходной функции соответствуют какие-то точки в конечной функции. Ничего не пропало и не убавилось. Всё просто поменяло своё исходное место при «деформации» исходной функции (параболы) синусом.
Это не просто круг:

Это бесконечно длинный цилиндр, обтекаемый боковым потоком жидкости. На самом деле это подводная лодка, вид с морды.
А это «заготовка» профиля крыла самолёта:

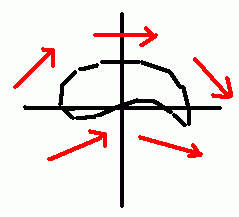
… когда её уже начали преобразованиями «деформировать» из круга, но пока ещё не успели сделать бесконечно тонкой.
Я, за давностью лет, могу ошибаться, но, по–моему, если итоговый профиль из начального можно получить конформным отображением, то все решения для таких профилей можно получать автоматом, применяя к решению для обтекаемого цилиндра ту же функцию, что применялась для преобразования профиля.
Т.е если было получено решение какой-то задачи с множеством точек в виде параболы, то к этому, уже имеющемуся решению, достаточно применить синус и ничего больше считать не надо (т.е не надо решать новую, отдельную задачу).
Это вызвано тем, что при всём внешнем несходстве контуры сходны и являются, в каком-то смысле, одним и тем же, только по разному «смятым».
Подробности тут («Лекции и гидроаэромеханике» со стр.140):
https://drive.google.com/open?id=0B3i2SFYLER0HWWVSSXd3WnJ0cTg

А сам используемый «гаечный ключ» разработан в ветви математического анализа (теория функции комплексного переменного).