Математический анализ
Сразу напишу, что я не знаю толком что это такое. И тем более не знаю, зачем это надо.
Если не ошибаюсь, вот это называется «фрактал»:
https://www.facebook.com/xan.rubtsov/posts/925201830903529
…т.е некая структура, которая никуда не исчезает при более детальном (с меньшим масштабом) её изучении.
Это всё из математического анализа, который у нас был исключительно в виде математического аппарата (набора инструментов для решения задач).
В своё время на факультете даже вдохновилась и сделала что-то вроде мультфильма, в котором функция постоянно перерисовывалась, масштаб менялся так, как будто взгляд всё приближается к графику. Возможно, функция была: |x| * sin(1/|x|). Чёрточки означают модуль, т.е абсолютное значение, т.е “-1” становится “1”, т.е знак минус убирается.
Если, например, взять функцию x*x*sin(x):
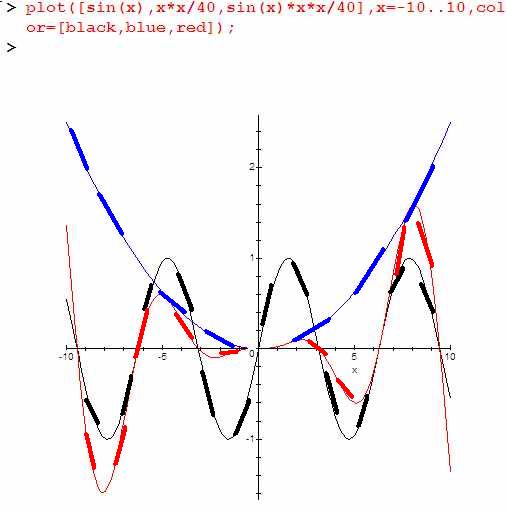
… то на диапазоне x от -10 до 10 она будет выглядеть как колебание, нарисованное красным. Обычный синус (чёрный) имеет постоянную частоту и амплитуду. Если его умножить на параболу (синяя = x*x), то его амплитуда начинает «примыкать» к параболе.
На диапазоне -1..1 от интересной картинки ничего не осталось:

Константы (40 и.т.д) здесь и ниже берутся исключительно для того, чтобы на картинке было что-то видно. В данном, например, случае виден только синус, а остальные функции уже слишком близки к нулю. Это картину можно было бы и исправить, поделив его, например на 3. На первой картинке его всё ещё было бы видно, а тут бы (из-за изменения масштаба графика) было бы чуть лучше видно и все остальные функции.
Данное действие – специфика математического анализа и вообще работы с бесконечно малыми и бесконечно большими. Функция 1/x ничем в этой логике не отличается от 1_000_000/x, потому, что миллион такая же константа как 1, а «перевесить» стремящийся к нулю x никакая константа не сможет. Обе функции уйдут на бесконечность при x близких к нулю (одна чуть быстрее, другая чуть медленнее, но это не важно, важно итоговое поведение).
А вот так можно сделать синус более интересным:
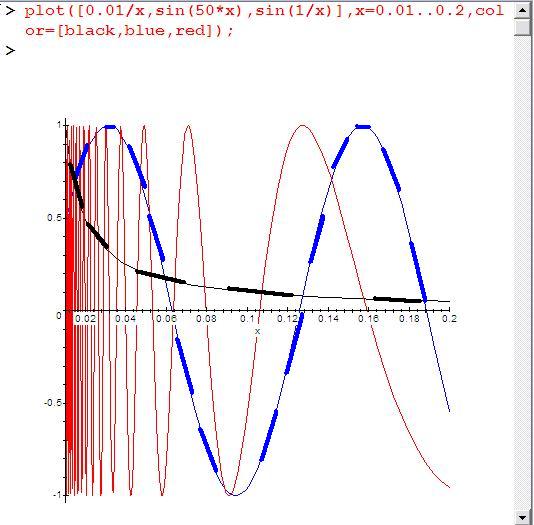
Обычный синус нарисован синим. Чёрным нарисована та самая 1/x, которая в окрестности нуля уходит на бесконечность. Если синусу это подсунуть в качестве аргумента, он с приближением к нулю начнёт увеличивать частоту. Итог нарисован красным.
На диапазоне -1..1 функция |x| * sin(1/|x|) имеет вид:
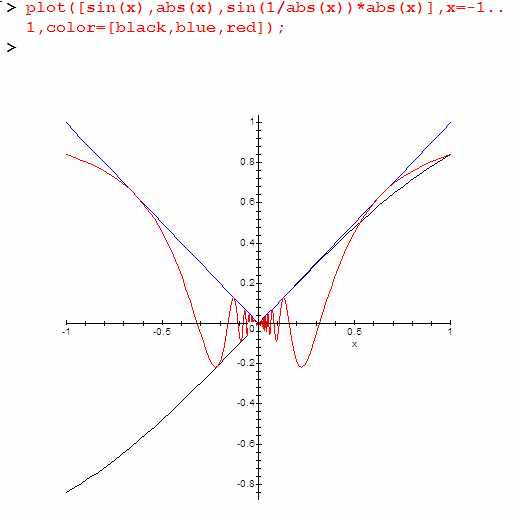
При «приближении взгляда», т.е при x=-0.1…0.1 колебания никуда не деваются. Становится так:
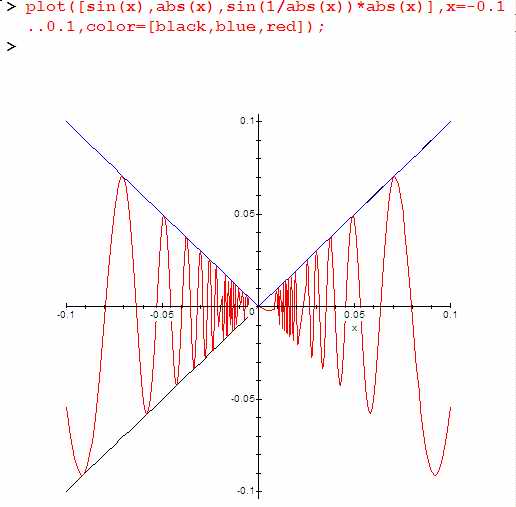
… и.т.д. Картинка по амплитудам с изменением масштаба не меняется. Это потому, что вместо параболы (x*x) взята прямая (x). А у прямой «скорость» при приближении к нулю постоянна. На графике это означает тот самый неизменный угол наклона, а в терминах производных это равенство первой производной константе x’ = 1, в то время как (x*x)’ = 2*x (т.е меняется при изменении x).
А вот как добиться того, чтобы картина по частотам не менялась не знаю. И даже не знаю, была функция, по которой делался мультфильм с постоянной частотой или частота увеличивалась как здесь.
Помню, что Подкорытов (седьмой слева, выглядывающий из-за усатого):
http://www.math.spbu.ru/analysis/staff_r.html
… глянул и сказал что-то вроде «Надо же, так мало масштаб изменился, но уже такая мерзость неописуемая». То ли это было про возросшую частоту, то ли там вообще что-то более сложное было, типа не гладкой функции, а чего-то с углами.
У меня о математическом анализе мало воспоминаний осталось. Тут нужны бОльшие способности к пространственному мышлению, как минимум. На первом курсе в первую сессию удалось всё это в себя чуть ни в виде картинки засунуть, в результате чего удалось получить трояк вдобавок к неизгладимому впечатлению.
Из таких случаев и возник анекдот: «Молодой человек, Вы что списываете??!! – Ээээ, кабы списывал, срисовываю».
Мои мозги так не гнутся. Потому, и не сообразить мне сейчас, что этому синусу надо подсунуть чтобы картинка покрасивее была. Скорее всего, если такое есть, то оно довольно простое.
Вот ещё пример:
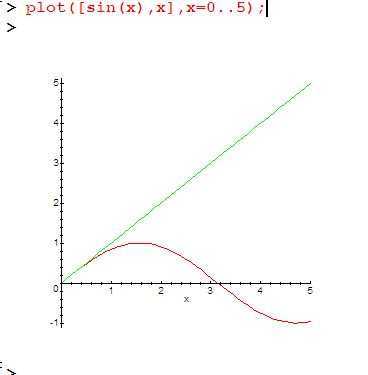
Синус это, естественно, волна, а x – это прямая. И ничего общего у них на таком диапазоне нет. Но в окрестности нуля они почти неотличимы:
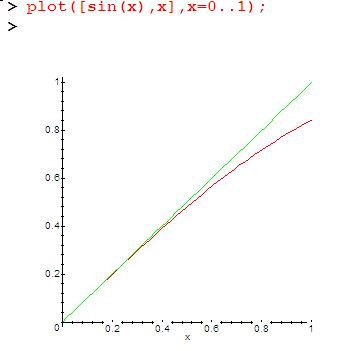
Их тождественность в районе нуля записывается разнообразно доказываемым и изображаемым:

… это не равносильные утверждения. Это две разные записи одного и того же.
Т.е никто их них при приближении к нулю не «перевесит». X может перевесить любую константу (включая тот самый миллион), но не убывающий с примерно той же скоростью синус.
Но отличие между ними конечно и в окрестности нуля есть. Sin(x) не равен x в окрестности нуля.
Sin(x) = x –x^3/3!+x^5/5!+….
http://www.pm298.ru/tei3.php
А это – разложение функции в ряд Тейлора. Это и есть часть математического аппарата, который и поставляет математический анализ всем, кому приходится изучать поведение функций. Не надо прикидывать, что там будет с этой функцией (как правило довольно сложной). Надо разложить функции в элементарные для расчёта ряды и посчитать порядок x. С остальными инструментами для расчёта и доказательствами неочевидного (которые есть в математическом анализе) примерно также.
Но это всё – достижения математического анализа 19-го века. Чем они сейчас занимаются затрудняюсь сказать. Вот это:
http://lesnik-201.livejournal.com/14015.html
… тоже часть математического анализа.
А вот поверхность со складкой:
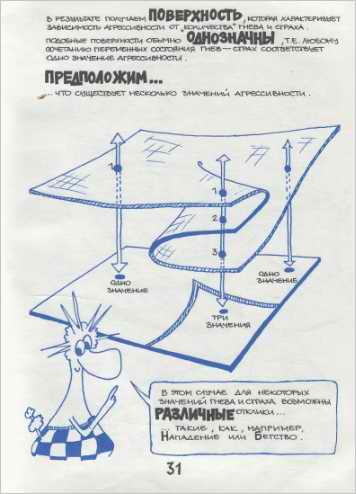
… из той же книжки. Свойство ленты Мёбиуса:
https://www.youtube.com/watch?v=J6EDsmt25vc
… тоже насколько понимаю можно вывести из каких-то формул, но чтобы со всем этим работать довольно специфические мозги надо иметь от природы. Здесь хоть что-то удалось в виде трёхмерной поверхности изобразить. А это далеко не всегда возможно. Ещё можно представить как себя будет вести в окрестности нуля синус с увеличивающейся частотой, хотя никто его глазами не видел и не увидит, потому что бесконечно малое не видно. А вот какую-нибудь поверхность типа бублик в пятимерном пространстве представить в своём воображении и ещё что-то про неё сказать это только для очень немногих.
p/s
«Теорию катастроф» может гляну чуть подробнее в ближайшее и время и что-то про ней ещё скажу. Пока не помню и не знаю, что там и про что там.
| 








