Математический ролик

По поводы этого:
https://zina-korzina.livejournal.com/1483466.html

Надо отдать должное, примерно с середины я правильно угадала, про что они пытаются говорить. Не уверена в том, что правильно угадала, почему это им вдруг потребовалась, но своя версия будет ниже.
Про множества чисел было тут:
http://akostina76.ucoz.ru/blog/2018-08-31-5348

… Конкретно по ссылке возможная версия того как додумались до множества комплексных чисел. Там помянуты множества:
1] Натуральнее числа (целые типа 1, 2, 3)
2] Рациональные числа – дроби, полученные делением натуральных друг на друга (впервые узнала про их существование, не вспомню ни одного использования этого множества)
3] Вещественные (они же действительные) – все числа в которых есть что-то после запятой.
Множество вещественных чисел – стандартное множество, с которым работает классическая современная математика.
Почти все теоремы начинаются с такой записи:

Тут написано: «Пусть существует функция f(x), такая что x из множества вещественных числе и f(x) из множества вещественных чисел»
Эта дежурная фраза чем-то напоминает стандартный бланк. Обязательно сверху есть название ведомства, а снизу фамилия и телефон исполнителя. Как правило, что-то и так понятно, а что-то никому не нужно. Но это пишут. И тут в самом начале пишут, с чем собираются иметь дело (т.е с множеством вещественных чисел).
Современная классическая математика – продукт физики, возникшей во времена Ньютона. Именно там потребовались дифференциалы чтобы считать скорости и интегралы чтобы считать расстояния.  А это всё хорошо работает  на гладких непрерывных функциях, т.е на тех самых множествах вещественных чисел без разрывов, дырок и т.д.
Но и из этой классики можно выдернуть пример не вещественных чисел. Песенка по синус, при том, что они её никак не прикрутили к прочему материалу, не совсем неуместна.
Синус это вот это:

Т.е это функция, которая болтается в коридоре от -1 до +1.
Если я собираюсь иметь дело с чем-то подобным, то мне никто не мешает написать так:

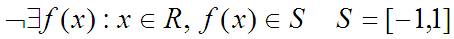
Здесь я определяю множество S – тот самый промежуток от -1 до +1 (т.е это ограниченное множество – кусок вещественного).  Обозвать выбранное множество могу любой свободной буквой. Важно, что я аккуратно пишу, с чем собираюсь иметь дело.
Теперь моя версия того зачем им это вдруг потребовалось. В компьютере нет никаких вещественных чисел. Там всё целое. Иногда оно только удачно притворяется вещественным. Но внутри там вообще только нули и единицы. Это, кстати, тоже вполне множество. Состоит оно из двух значений. Почему ему не быть если есть некая область человеческой деятельности, где в множестве есть только два эти значения?  Никто не заставляет сидеть в множестве вещественных чисел. Точно также раньше вышли в множество вещественных потому что рациональных вдруг стало мало (для новых задач).
И в этой компьютерной деятельности есть простая задачка – линию нарисовать на экране. Казалось бы, всё просто – считать значения по теореме Пифагора и рисовать точки на экране. На самом деле это, для начала, очень тяжелая математическая задача. Компьютер считает, конечно, быстрее чем человек, считающий на бумажке в столбик. Но это серьёзная нагрузка. К тому же неизбежно получаемые не целые результаты придётся округлять чтобы красить на экране точки, координаты которых – целые числа.
Потому в компьютерах для решения этой задачи используется Алгоритм Брезенхэма:
https://ru.wikipedia.org

… позволяющий получить нужный (не «тот же», а результат в множестве натуральных чисел!) хотя бы без вычисления корней.
Это переход из вещественных в дискретные множества. Т.е даже не в натуральные числа, которых бесконечно много, а в кусок натурального множества потому что и экраны имеют конечные размеры и цветов точек (обозначаемых цифрами) хоть и много но тоже не бесконечно много.
Именно про эту дискретность (т.е про то, что функции это не только что-то привычное и гладкое) и пытаются, по-моему, рассказать.

Второе возможное направление – это статистика. Размер армейских сапог не бывает ни отрицательным, ни 80-м. Но, по-моему, в теории вероятностей множество событий и так очевидно из целых состоят. И определение функций я там не помню (не факт, что их там нет, просто плохо помню этот предмет). Какие-нибудь нормальные распределения это приближение и это, вроде, не то. И сама вычисляемая вероятность это не то,  ведь интересует понятие функции как зависимости одного набора от другого (и какие-то действия со всем этим).

.