Определение общих свойств по небольшой выборке

Пример с дегустаторами вин:
https://akostina76.ucoz.ru/blog/2019-04-14-5782

… заставляет вспомнить такой показатель как «Индекс физического объема ВРП», т.е рост или спад экономики. Действительно, в примере с винами качество вина улучшалось со временем. А этот экономический показатель определяет улучшилось (ускорилось) или замедлилось экономическое развитии. Вроде бы использованный метод хорош для того чтобы понять произошли ли принципиальные изменения в экономике или зафиксированное изменение в какую-то сторону своеобразная статистическая погрешность.
Но пожалуй, всё-таки, пора остановиться и вспомнить для каких целей выводились все эти формулы. В случае дегустаторов вин предполагается что есть некое общее свойство у всех вин. Его-то и хочется узнать. Занять этим исследованием тысячи людей невозможно. Можно отобрать 10 или 20 человек  При некоторых условиях эта информация может считаться правильной для того самого всего вина, которое исследовать невозможно.
В случае же индекса роста экономики мне и в голову не приходит распространять результаты на индийские провинции и американские штаты. А придуманный и используемый инструментарий что-то мог бы дать именно в такой задаче.
Если такой задачи определения общемирового значения по небольшой выборке нет, то формулы-то использовать можно, но не очень понятно как интерпретировать полученный результат.
t-оценка по двум выборкам это явно какой-то интеграл пересечения двух горок. Но первое что хоть как-то надо объяснить это замена обычного разброса S на суженный S_M.
S_M это отклонение (ошибка) средней. Пусть есть много выборок по срокам беременности. В каждой по 10 человек. Для каждой из этих выборок можно посчитать какое-то среднее значение. Если выборок много, что уже по этим средним можно нарисовать частотное распределение типа такого:

Ширина горки (S_M) естественно будет меньше чем S (отклонение – разброс) всех сроков по выборкам. Именно это сужение ширины позволяет получить тонкие графики, и сделать какие-то выводы по тому, пересекаются они или нет.
В случае сроков беременности действительно проводилось много выборок. В случае дегустаторов только одна, но формула для S_M сжимает график так как было бы для средних значений при многих выборках.
Информация по индексу по субъектам – уже просуммированная информация. Так что сужать распределение переходом от S к S_M строго говоря нет никакого основания. Я, во всяком случае не могу придумать почему это можно было бы сделать.
А вот делать ли какие-то выводы по такому виду расположения данных за 2009 и 2010 год:

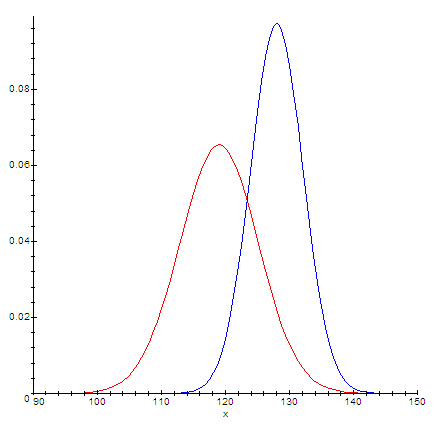
… не знаю. Вопрос вкуса. И тут можно придумать какую-то небольшую площадь пересечения, которая всё ещё считается отсутствием изменений.
Но строго говоря это использование инструмента не по назначению. Инструмент при этом выдаст какой-то результат. А вот как его интерпретировать – большой вопрос. В случае горок для индексов это точно не вероятность, но тоже может быть полезно.
p/s
По статистике пока всё. Большие наборы данных требуют учета размеров. Потому мне показалось что без этих статистических инструментов уже никак. С другой стороны всё что меня интересовало я уже прочитала. Уже можно и остановиться.
Книга целиком тут:
https://drive.google.com/open?id=0B3i2SFYLER0HMEticUVTU1JVdEU

: