Переходные процессы в QUCS (зарядка конденсатора)

Переходные процессы это когда обычного переменного тока ещё нет, а изменения токов и напряжений со временем уже есть. 
Так и не заработавший мультивибратор:
http://akostina76.ucoz.ru/blog/2018-11-23-5514

… должен был быть таким переходным процессом (с переменным напряжением на светодиодах).
Схема для моделирования будет довольно простой:

Чтобы всё отработало, надо только не забыть установить начальное напряжение на конденсаторе в ноль.
Намоделирует он такие ток и напряжение:

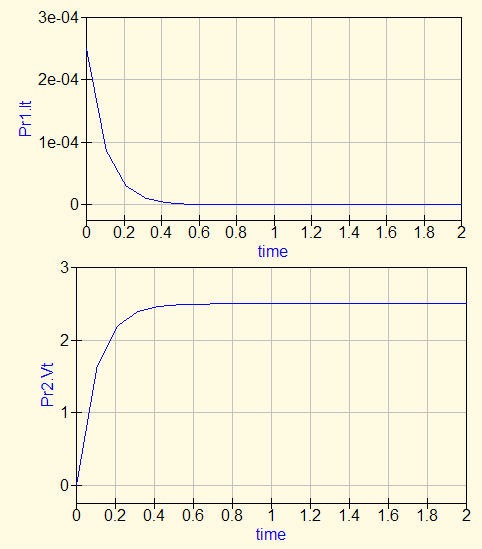
А вот то, что там происходит не совсем тривиально. Потому, наверное, стоит разобраться и сформулировать. В схеме батарейка заряжает конденсатор с ёмкостью 10 мкФ через сопротивление 10 000 Ом.
Общеизвестное, добытое из всякой «википедии»:

Это всё, конечно, очень интересно, но меня, как бы, интересуют функции от времени I(t), U(t) и общее время за которое этот конденсатор зарядится при такой зарядке. По сети бродит формула T(время)=10*R*C загадочного происхождения и без объяснений.
Пришлось немного покрутить всё это в руках, получить интегральное уравнение и решить его.
Для начала очевидное (подставляю одно уравнение в другое):

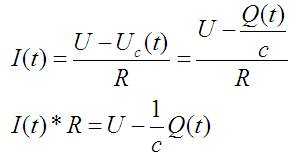
Осталось вспомнить, что накопленный на конденсаторе заряд Q это сумма всего тока, который в него втёк (т.е интеграл от тока по времени). Получается то самое интегральное уравнение:

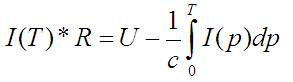
Я не помню, как дифференциальные уравнения решать. А интегральных (т.е с интегралом в не дифференциалом) вообще «не бывает». Допускаю, что всё это можно продифференцировать и решить, но не уверена, что смогу это всё сделать достаточно аккуратно.
По счастью, ответ тут довольно легко угадывается. Это явно какая-то экспонента с отрицательным аргументом. Все её коэффициенты тоже легко подгоняются. Такая там функция:


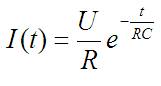
На всякий случай подставлю в выражение и докажу что ответ правильный:

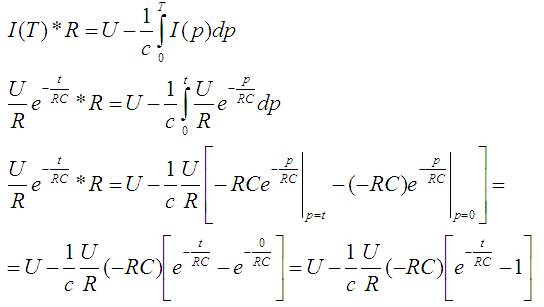
Здесь всё сокращается:

Напряжение на конденсаторе (зависимость от времени) теперь тоже можно записать:

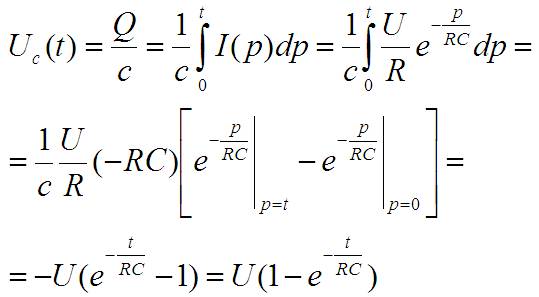
А теперь интересно, когда напряжение на конденсаторе достигнет напряжения на батарейке. Самое интересное, что никогда. В бесконечно удалённой точке времени:

Натуральней логарифм (ln) это вот такая функция:

Время по строгой математике бесконечно, а конденсаторы вполне себе заряжаются за конечное время. Чтобы посчитать надо чуть снизить математическую точность и считать конденсатор заряженным когда на нем уже какая-то довольно большая доля напряжения батарейки:

Пусть k=0.9, т.е а конденсаторе 90% заряда батарейки. Тогда логарифм равен «-2.3». А загадочной цифрой 10 (найденной в интернете) логарифм становится  при напряжении 0.9999 от батарейки (ln(0.0001) = -9.21).
Осталось проверить все эти рассуждения на QUCS схеме. Вот такие результаты моделирования:

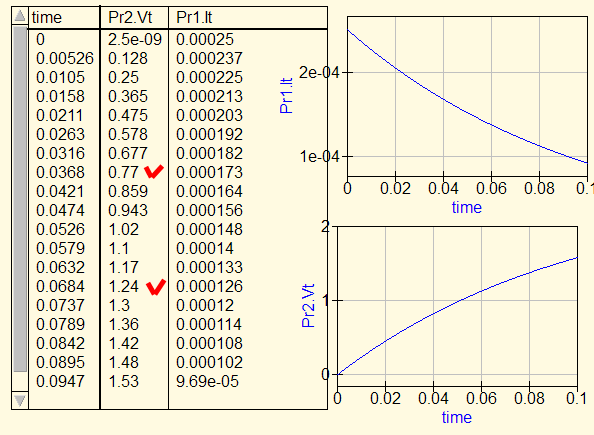
Половина напряжения батарейки это 1.25, а 30% это 0.75. Если подставить эти k в формулу для времени зарядки:

В таблице это время 0.0684 и 0.0368. Очень прохожее на то, что в расчёте.
Схема тут:
https://drive.google.com/file/d/19YgqATBA48wSELdM5pXekDc3meHp-B-E/view?usp=sharing