Примерные формулы, описывающие кровоток

Когда чего-то делаешь, лучше хотя бы примерно понимать зачем. Тогда, с одной стороны не будет ощущении бессмысленности, а с другой не будет завышенных ожиданий.
Обилие сосудов делает задачу реального подсчёта всего, чтоб всё состыковалось до миллилитра крови, ни то чтоб нерешаемой, но в данном случае явно ненужной. Ниже я собираюсь скорее поиграться с цифрами, чем что-то рассчитать.
Реально важны скорее биологические моменты, которые накладываются на типовые схемы физических расчетов и, как ни смешно, делающие их непригодными для практики. С другой стороны, физические методы дают схему, на которую можно повесить всю информацию (включая биологическую специфику).
Схема движения крови:

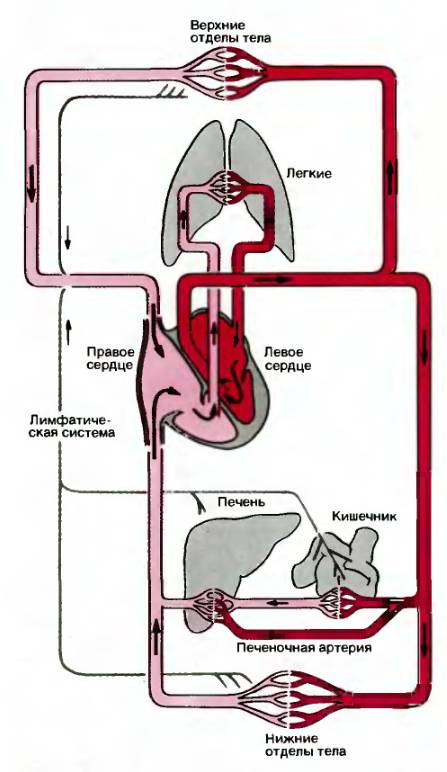
.. в которой самое интересное то, что кровь, прошедшая через органы кишечника потом проходит через печень.
Движение крови можно описать формулой, похожей на закон Ома для электричества:

Разность давлений тут ассоциирована с разностью напряжений батарейки. Разность обычно это одна батарейка, прицепленная плюсом и ноль на другом конце. В кровеносной системе примерно то же самое, т.е сердце вбрасывает кровь в артерию, а по венам она уже сама дотекает обратно (ничто её не втягивает и не отталкивает). .
Важно тут то, что батарейка может быть одна и та же, а работа схемы будет определяться тем, из чего она состоит. А если состав и подключение неизменно, то сопротивлениями отдельных элементов. Батарейка – насос – сердце выдаёт примерно такую мощность:

Если при одинаково работающем сердце уменьшилась скорость движения крови по сосудам, то логично предположить что увеличилось сопротивление кровеносной системы R (также как и в случае электрической схемы).
Проталкивать воду через тонкую трубу тяжелее, чем через толстую, потому сопротивление отдельного более мелкого сосуда больше чем сопротивление крупной артерии. Но поскольку самих таких мелких сосудов после разветвления больше, то общее сопротивление участка мелких сосудов может быть даже меньше (и падение напряжения на этом меньшем сопротивлении будет меньше):

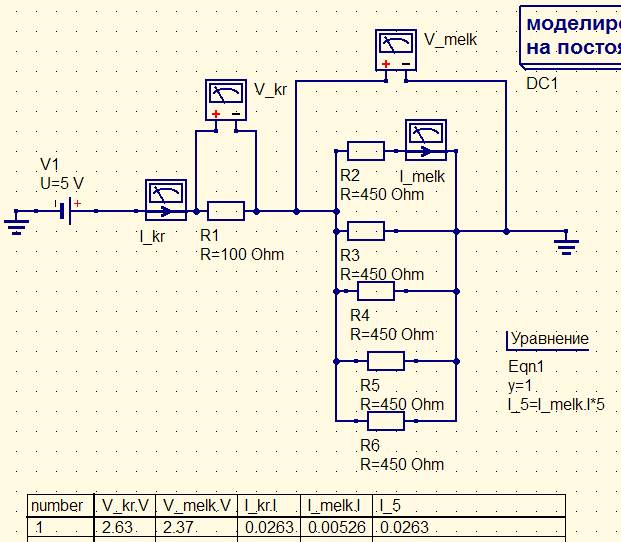
В этом месте простая аналогия с электричеством ломается потому что, следуя этой логике, давление выдаваемое сердцем должно быть равно сумме давлений в сосудах разного типа, а это не так:

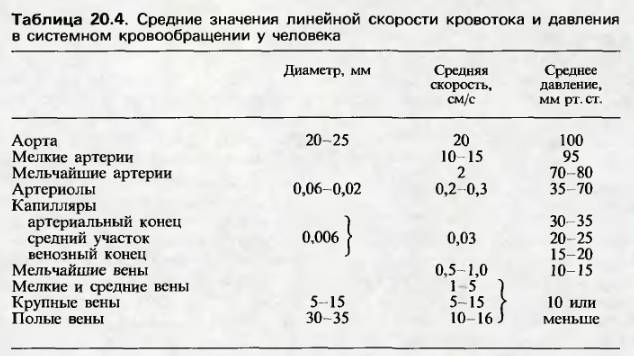
Некоторые вещи можно сформулировать как закон (т.е наблюдаемое и можно без объяснений). В данном случае утверждается что объемная скорость (V_об) при кровотоке постоянна, а при изменение диаметра сосуда меняется линейная скорость кровотока:

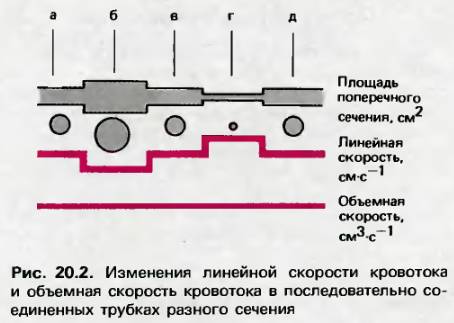
… т.е в более тонких сосудах для сохранения прокачиваемого объема увеличивается линейная скорость.
А теперь про то, что ближе к практике, про вязкость крови. Кровь - вязкая жидкость. Да и стенки труб – сосудов не обязаны быть идеально гладкими.
При протаскивании жидкости по сосуду возникает такое же трение как и задаче о санках, которые тащат по снегу:

… т.е противодействующая сила трения F_тр, пропорциональная какому-нибудь коэффициенту трения k. Точно такое же трение возникает в вязкой жидкости между слоями этой жидкости. Они тоже при движение трутся друг о друга.
Всё то, что происходит в подобных средах, принято описывать на языке закона Гука для упругого растяжения стержня (растягиваемого какой-то силой). Вот так это обычно пишется:

… применительно к такой задаче:

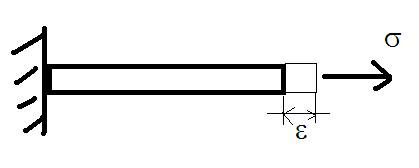
Вот так это выглядит на графике в упругом случае растяжения:

Даже стержень можно не только растягивать или сжимать. Его можно гнуть или скручивать. В общем случае простая формула с одним коэффициентом становится системой уравнений, а коэффициент E матрицей из 9 цифр, но само соотношение напряжений и деформаций сохраняется, только уже в векторное- матричном виде.  Т.е всегда между какими-то напряжениями и вызванными ими деформациями находятся какие-то коэффициенты.
Для напряжений и деформаций именно сдвига (возникающих при вязкости) используются немного другие буквы и закон записывается так:

Так вот, проблема заключается в том, что нет тут никакого постоянного коэффициента (ни упругости, ни пластичности как для стержня).
Диаграмма выглядит примерно так:

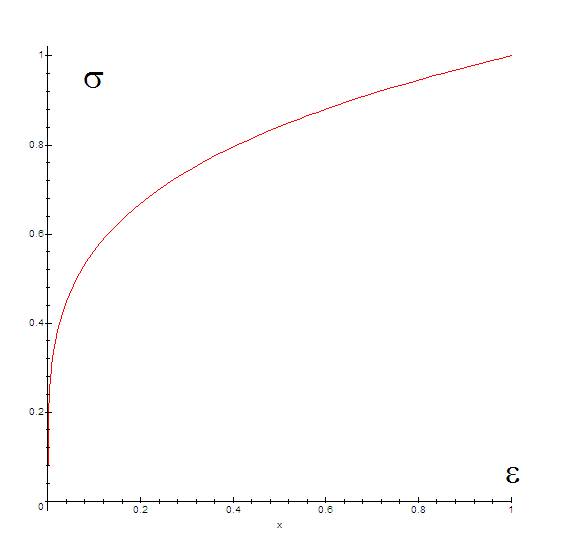
… т.е вязкость резко увеличивается при снижении скорости кровотока. Низкий кровоток это уже что-то ненормальное, а это свойство крови ещё усугубляет ситуацию (повышая вязкость и увеличивая сопротивление).
Вызвано это вот чем:
Повышение вязкости крови при замедлении кровотока объясняется обратимой агрегацией эритроцитов, образующих скопления в виде монетных столбиков или прилипающих к стенкам сосудов. Агрегация эритроцитов обусловлена наличием в плазме крупных белков (фибриногена, а2-макроглобулина и т. д.). В патологических условиях тенденция к агрегации может настолько возрастать, что для продвижения крови требуется дополнительная энергия. Кроме того, при высоких скоростях кровотока эритроциты изменяют свою форму и соответствующим образом ориентируются по ходу струи; увеличение вязкости крови при низких скоростях кровотока частично обусловлено отсутствием этих эффектов
… Т.е в крови есть эритроциты, а они склоны слипаться при низких скоростях. Вот такое неотменяемое свойство даже не сосудов, а текущей в них жидкости. Хотя процесс может быть запущен и сужением сосудов и недостаточной работой сердца.
Одним из симптомов в 2016-2017 году было странное состояние, которое почему-то снимаемое прогулкой. Скорее сего дело было в том, что сопротивление сосудов повысилось и кровоток при отсутствии физической нагрузки падал. А потом уже свойство крови ещё ухудшало ситуацию. А физическая нагрузка, так или иначе, разгоняла кровь и потому резко улучшала ситуацию.