Расчёт вероятности вручную, дисперсия

Пример добыт тут:
https://deoma-cmd.ru/files/sets/EGE-GIA

В этом примере настолько мало данных, что можно всё подсчитать вручную. Причём, что интересно, вполне точно. У монетки две стороны, значит возможных комбинаций:

Если бы был кубик, то было бы N=6^n, потому что у кубика 6 граней.
Вероятность конкретной последовательности, например, вначале орёл а потом решка в данный момент никого не интересует. Но может уместно написать, что она равна =1/N, потому что в списке возможных комбинаций нет повторяющихся вариантов.
Интересует насколько вероятно что решка выпадет один раз. Не важно, так будет  «орёл + решка» или так «решка +орёл». Важно что будет 50% решек, или половина всех вариантов (вероятность = 0.5).
Расчёт можно так нарисовать:
 

Перечислены все комбинации и просто подсчитано, какие из них содержат только одну решку. Таких две.
Интересно, что довольно таки невероятное для монеток событие одних орлов или решек имеет тут вероятность аж 25%. Причём это точная оценка, никаких приближений тут нет, при двух подбрасываниях так и будет. Т.е чем меньше данных тем меньше видно отличие обычного от необычного, тем хуже работает статистика как метод.
Очень удобно то, что орлов и решек легко заменить на двоичную систему счисления. Орёл «О» становится нулём, а решка «Р» единицей. Ряд нулей и единиц в двоичных числах столь же уникален как и в десятичных и точно также последовательно вытаскивает все комбинации.
Функция перевода десятичных числе в двоичные для Excel-я:
' MsgBox DecToBin(10, 32)
Private Function DecToBin$(ByVal i&, Optional l% = 16)
Dim x As String
Do While i > 0
    x = i Mod 2 & x: i = i \ 2
Loop
DecToBin = String(IIf(l, Abs(Len(x) - l), 0), "0") & x
End Function
Хоть какая-то автоматизация позволяет увеличить число подбрасываний монетки до 4-х и довольно легко всё подсчитать:
 

По этому небольшому набору уже вполне можно нарисовать стандартный для этого случая график:

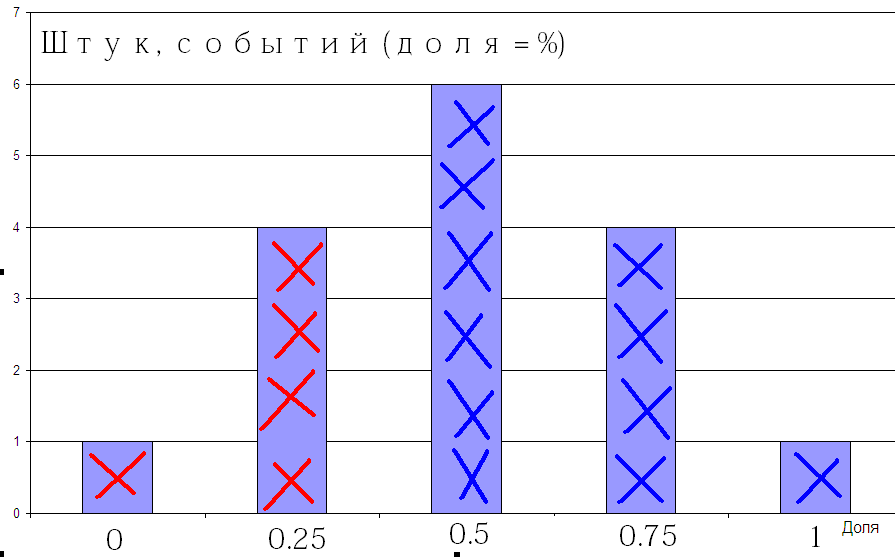
25%  единиц было в 4-х случаях. 25% или меньше в пяти. Это и есть вероятность редкой комбинации. Но ведь это же и площадь под графиком. Можно нарисовать и так:

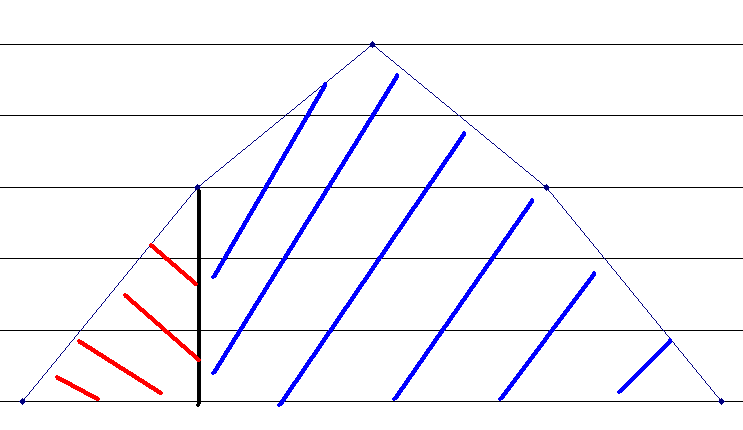
Площадь под графиком – интеграл функции на каком-то диапазоне горизонтальной оси. Т.е даже для очень больших объемов данных есть вполне подходящий инструментарий интегрирования, который и придумывался для того чтобы суммы многих мелких столбиков проще было считать.
По графику видно что распределение частот тут – симметричная гора. Есть все основная думать, что случайные величины лежаться на график так называемого нормального распределения.
Вот его функция:

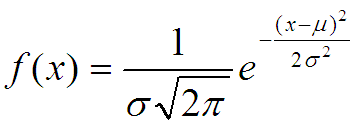
Тут много чего понаписано, потому вначале самый простой вид функции который похож на ту гору, которая мне нужна:

Первое, что мне тут совсем не нравится это то, что вершина горы находится в нуле. Для моего случае в монеткой она должна быть при x=0.5.
Сдвигаю график:

Величина сдвига μ, которая тут равна 0.5 называется по-разному:
1] мода распределения
2] медиана распределения
3] математическое ожидание.
Получилось. На графике с крестиками количество крестиков у меня было равно 16, т.е количеству возможных комбинаций. Все 16 крестиков это 100% или вероятность равная 1 (= 16*(1/16)). Точно также и тут я хочу чтобы площадь под графиком была равна единице, а она для этой функции равна корню из ПИ:

Неприятно, но не смертельно. Чтобы получить единицу я просто поделю эту функцию на корень из ПИ:

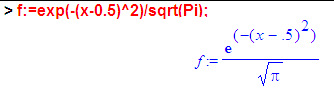
Уже получилось нечто довольно близкое к стандартной формуле нормального распределения. Но там ещё пририсован параметр σ.
Чуть поиграюсь с этим параметром чтобы понять как он влияет на вид функции – горки:

При k=0.5, 1 и 1.5:

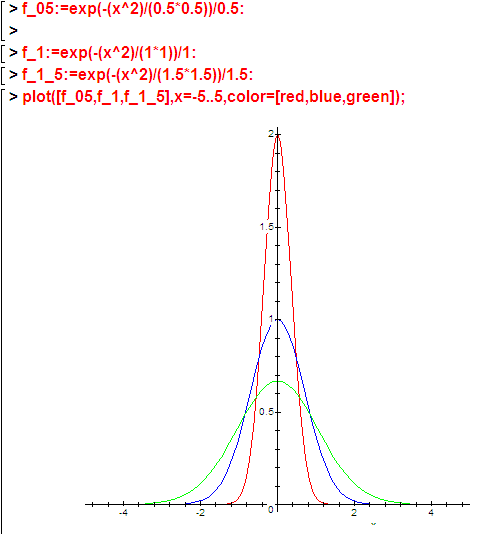
Чем меньше k тем уже горка, т.е тем ближе значения к среднему. Пусть, например, средний процент по расходов по какой-то статье 30% или 0.3. Для разброса значений от 25% до 35% k будет меньше чем для разброса от 20% до 40%.
По названиям:
σ- среднеквадратическое отклонение
σ* σ – дисперсия.
Расчётная формула:

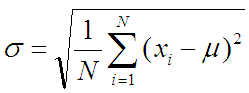
Сама формула – стандартный способ борьбы с отрицательными числами. Ведь отклонение от величины 0.5 может быть и положительным (0.75-0.5=0.25) и отрицательным (0.25-0.5=-0.25). Если их просто так просуммировать то они обнулят друг друга. А интересует всё-таки сумма отклонений во все стороны. Потому вначале все отклонений возводят в квадрат (чтобы всё стало с плюсом), а потом уже извлекают корень из суммы (чтобы вернуть осмысленное значение отклонения, а не его квадрата).
Надо сказать, что если аккуратно всё подсчитать и попытаться приблизить график с 16 значениями (крестиками) функцией нормального распределения то получатся отклонение расчётной вероятности (от посчитанной по крестикам) в два раза (такое ощущение что эта двойка где-то угуляла в выкладках). Не знаю в чём там дело, но пока ведь я рассказываю про то что такое дисперсия))).
Хуже то. что будет дальше. Ведь во вчерашнем примере:
http://akostina76.ucoz.ru/blog/2019-03-19-5725

… у меня монетка подбрасывается 30 раз. 2^30 = 1 073 741 824 комбинаций. Ни в какой Excel это уже не влезет. Большой объем информации, вроде, позволяет задействовать интегралы вместо подсчёта крестиков. Моду я знаю, диапазон интегрирования знаю, вид функции знаю. А вот дисперсию я не знаю. А без неё я вероятность (как интеграл от функции) не получу (я не знаю точно какая у меня функция).
Пример про монетку это просто задача, которую как-то надо решать. Попадает такая задача к человеку с базовым математическим образованием и он начинает её как-то крутить, прикидывая какой инструментарий тут можно использовать. И получается что напрямую тут как-то ничем и не ухватиться. Не говоря уж о том, что правомерность замены столбиков – крестиков примерно похожей по виду функцией неплохо бы и доказать. Так и начла развиваться отдельная наука (теория вероятности, статистика), с отдельными выведенными формулами и математическими доказательствами.
Добавлю сюда же что функция нормального распределения, вообще-то, не интегрируема. Т.е получить её интеграл в виде привычных синусов и косинусов нельзя. Но уж слишком часто нужна она и её значения. Потому придумали так называемую функцию ошибок erf:

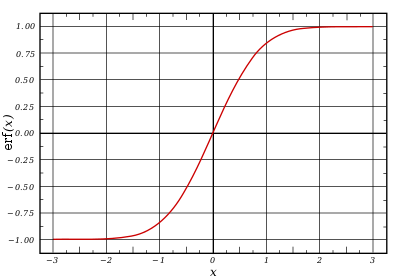
Значение этой функции в конкретной точке X – вероятность события. При доле 0.25 это какое-то небольшое значение. При доле 0.5 больше. Ведь вероятность в этой точке  это уже вероятность значений из половины диапазона. На правом же края диапазона значение функции равно 1, потому что все возможные значения уже попали в диапазон.