Способ выявить разные группы

От телефона требуется связь. От компьютера - умение быстро считать. Довольно часто от какой-то области знания требуется просто выдавать простые но точные ответы на какие-то вопросы.
Конкретно от статистики может потребоваться обоснованный и точный ответ на вопрос» “Разные предметы описывают два набора цифр или один и тот же?”. Например, с двух разных полей собрали урожай:

https://akostina76.ucoz.ru/blog/2019-03-29-5743
Взяли пробы из 10 разных мешков для каждого поля. В одной выборке одни проценты овсюг/пшеница, а в другой – другой. Какова вероятность того, что так получилось случайно? Потому что если такое не случайно, то можно уже выяснять дальше. Что сеяли? Чем могут отличаться условия, раз результат получился разный? Но пока нет более или менее обоснованного ответа на вопрос разные эти результаты или нет, нет повода и разбираться.
Тоже самое с чем угодно другим, например со случайными и не случайными поломками. Полезен инструмент, позволяющий выявлять необычные «пятна» в происходящем, отличая их от редкого но всё-таки вполне возможного по естественным причинам.
Ниже будут расчётные формулы и пример расчёта. Откуда формулы на этот раз не знаю. Без понимания откуда такое взялось, процесс начинает походить на шаманизм. Но разбираться в деталях вывода (откуда такие формулы и такие цифры) у меня сейчас нет настроения.
Пшениц и овсюгов у меня под рукой нет. А есть у меня информация по количеству автомобилей на 1000 человек. Вот у меня и возникло желание сравнить два участка земной поверхности по засеянности автотранспортом. Сравнивать я буду… Латинскую Америку с центром и югом России.
Причина такого выбора – эта частотная характеристика:

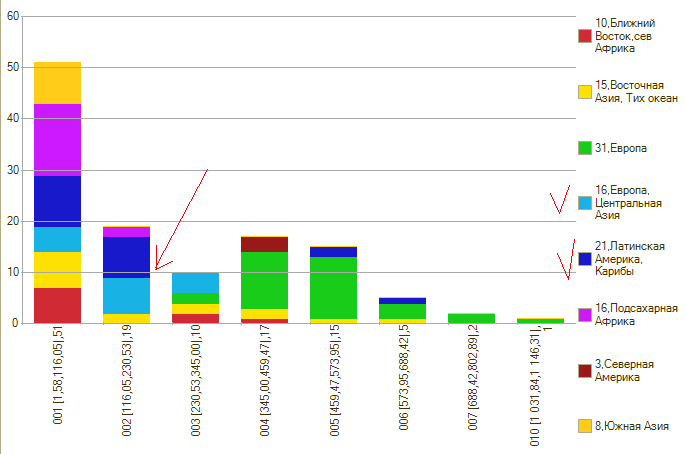
… в которой мы – соседи.
Сразу возникает проблема. Сравнивать надо одинаковое количество чисел, а в Латинской Америке только 21 страна, для которой есть информация по автомобилям. Поскольку я сейчас занимаюсь демонстрационной дурью, я вполне могу выбрать для сравнения любые субъекты. Главное чтобы их было 21. По соображениям элементарного приличия а решила выбрать соседей, т.е. не отдельные Чукотку с Ингушетией, а юг с часть Центрального федерального округа. Часть потому что целиком их слишком много. Юг потому что Америка Южная))).
Вот эти выборки:

 Формулы:

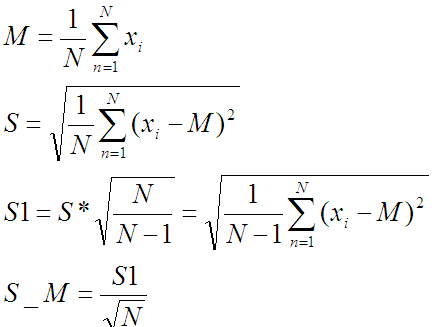
У нормального распределения две константы, определяющие его форму. Среднее арифметическое μ и среднеквадратичное отклонение σ.
Проблема в том, что тут у меня не бесконечное количество информации и даже не очень больше. Жалкие цифры в количестве 21 штуки. Потому точность этой информации под большим вопросом. Чтобы хоть как-то повысить качество и используются S1 и S_M вместо обычных для больших выборок S, посчитанных стандартным образом. При сравнении будет использоваться S_M.
С графической точки зрения более точное S_M сильнее всего прижимает допустимые значения к среднему:
mu:=190.43:
s:=46.5270647:
f_s:=exp(-((x-mu)^2)/(2*s*s))/(s*sqrt(2*Pi)):
N:=21:
s1:=s*(N/(N-1))^(1/2):
S_M:=s1/( N^(1/2)):
f_s1:=exp(-((x-mu)^2)/(2*s1*s1))/(s1*sqrt(2*Pi)):
f_s_m:=exp(-((x-mu)^2)/(2*S_M*S_M))/(S_M*sqrt(2*Pi)):
plot([f_s,f_s1,f_s_m],x=0..300,color=[red,blue,black]);

Если графики для S и S1 почти не отличаются, то замена на S_M сжала распределение очень сильно.
Формула для t-оценки без учёта корреляции:

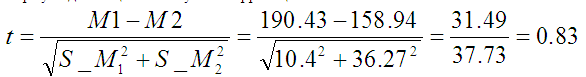
Это очень похоже на формулу для Z-оценки. Можно сказать, что одно среднее (пусть M2) тут выбрано за среднее, а второе (пусть M1) за X. С изобилием аж из двух среднеквадратичных отклонений справились взяв средний квадрат уже от них (почему на 2 не поделили, не знаю).
Графики двух распределений с отклонением S_M выгладят так:

Посчитанное значение t – цифра как цифра. А вот вид графиков заставляет усомниться в том, что в формулу засунута корректная информация. Ведь мне хочется увидеть сходство или различие, а вид информации (разброс) уж очень разный.
Но продолжу демонстрировать метод. Осталось мне по этому значению t определить вероятность того, что такое значение получено случайно.
В этой таблице:

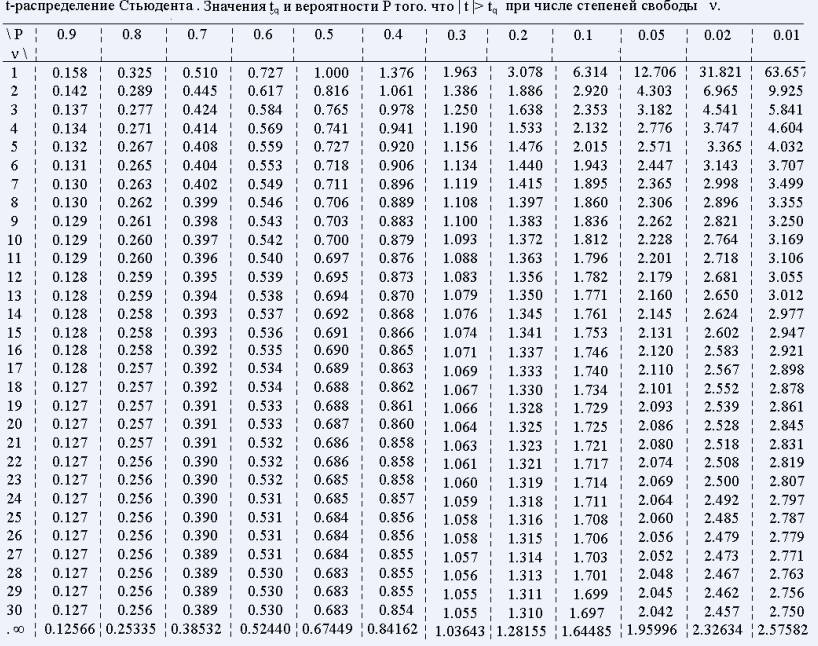
Или в этом куске:

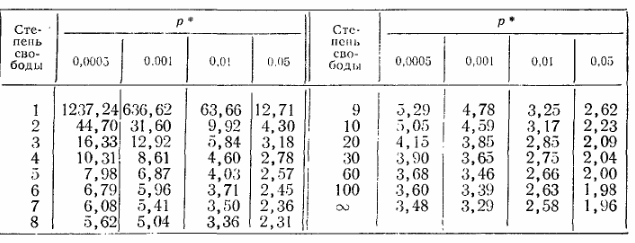
…надо найти подходящее значение t в строке с N-1 (степень свободы). В данном случае меня интересует строка с номером 20, а значение t у меня между 0.687 и 0.870. Вероятность того, что такие данные получены случайно – значение p в первой строке. Для этих выборок между 0.4 и 0.5, т.е весьма вероятное событие.
Посчитанный результат означает что выбранный кусок России от Латинской Америки не отличается. Т.е если случайно получены такие цифры,  то весьма вероятно что эти цифры описывают одинаковые по этому цифровому параметру объекты.
А теперь покажу, как будут выглядеть на графике разные объекты. Если я по Латинской Америке возьму такой же разброс как по России, то графики будут выглядеть так:

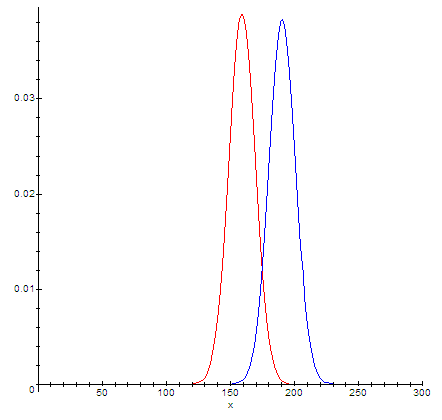
Теперь синий график уже не целиком входит в диапазон красного. Пересекается только часть диапазонов. Значение t = 2.15. А значение вероятность случайности p=0.05. p мало значит это разные описания разных объектов. Пересечение графиков уменьшится и в случае если средние значения (координаты вершин горок) будут больше отличаться.
Если бы по российским субъектам среднее было 290, то широкий и разброс по Америке не дал бы пересечения функций:

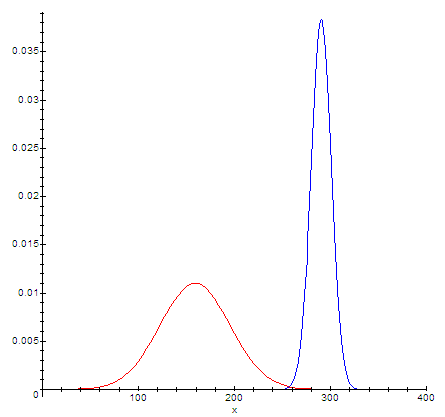
Оценка t была бы равна 3.48 (вероятность явно меньше процента).
Попросту говоря, оценка t определяет насколько горки распределений похожи друг на друга, т.е даёт числовую оценку этой похожести. Если похожи, то две выборки – описание сходных объектов (p – велико). Если не похожи, то цифры получены по разным объектам (p мало).
Результат получен, но не нравится он мне хотя бы с эстетической точки зрения. Ведь одинаковость явно означает сходство графиков а они у меня разные по разбросу. В данном случае дело, думаю, в том, что в Америке в рассмотренных странах проживало в 2009 году 478 млн человек, а в выборку российских субъектов у меня даже Москва с Петербургом не попали (т.е порядка 40 млн населения в выборке). Это такое сравнение нескольких «мешков» с целым «зернохранилищем». Естественно, что разброс значений по массе вариантов поглотил небольшую выборку, показав, что и такое (в пределах большого разброса) тоже запросто может быть.
Поучился ещё один пример того как важно следить за корректностью данных до того как начались расчёты.
Добавлю сюда, что если данные меняются синхронно (т.е коэффициент корреляции близок к 1 для двух наборов данных), то это тоже надо учитывать при вычислении t. Формула в этом случае меняется на такую:
 
 

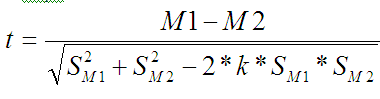
… где k – коэффициент корреляции.
При всех проблемах описанного примера, если с постановкой задачи всё в порядке, т.е сравниваются именно «мешки» с «мешкам», то описанный инструмент должен выдавать очень полезный в хозяйстве результат.