Суммирование изменения свойства по объёму
Здесь было про то, как считать изменение какого-то параметра (температуры, плотности и т.д) в конкретной точке:
https://akostina76.ucoz.ru/blog/2020-08-04-6662
… а очень многие законы говорят о том, что общее изменение какой-то величины по объему равно нулю или какой-то известной величине.
Закон сохранения массы, например:
https://akostina76.ucoz.ru/blog/2020-07-29-6656
… утверждает, что молекулы, которые были в каком-то объеме, никуда не исчезают и неоткуда не возникают.
Казалось бы, можно этот закон записать так:

.
Есть меня начальное и конечное значение массы M как интеграла плотности по объему. Их равенство это приравнивание интегралов. Приравнивание интегралов равносильно равенству нулю производной по времени (т.е изменения). Ничто не мешает мне поменять местами интеграл с дифференциалом, т.е внести d/dt под интеграл. Равенство интеграла нулю по любому объему возможно только при тождественном равенстве нулю подынтегрального выражения. Значит, изменение плотности – тождественный ноль, осталось посчитать его по всем правилам (по правилам дифференцирования сложной функции).
Логично? Вроде да. Правда, вывод получился несколько парадоксальный. Последнее выражение означает, что плотность воздуха (или жидкости) нигде, никогда, ни при каких обстоятельствах не меняется. Как-то это не очень стыкуется с представлениями об этой среде.
То, что написано выше – пример того как вроде бы равносильные переходы являются ошибочными. Так тоже может произойти. Это – не арифметическая ошибка, но нечто к ней довольно близкое. Потому что с того момента как декларировано нечто типа того что выше, модель происходящего приобретает новое свойство. Это свойство никак не следует из закона сохранения массы.
С этого момента может произойти что угодно, потому что из неверного утверждения следует что угодно (это тоже своеобразный закон)..Шуточный пример для запоминания «если дважды два – пять, то все черти зелёные». Я не знаю, куда меня приведёт тропинка, начавшаяся с утверждения что закон сохранения массы равносилен закону сохранения плотности, но выводы точно будут неожиданными и даже сенсационными. Только к реальности, увы, они точно уже не будут иметь отношения.
А получилось так странно, потому что мне лень было приписать буквы – объемы под интегралами. Так надо писать:
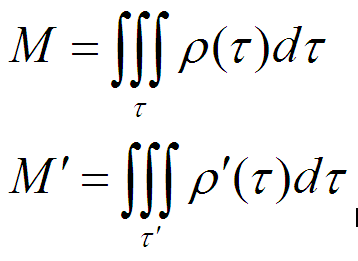
Т.е учесть, что газ и жидкость могут менять форму. На тех самых защитах, на которых сидят специалисты, если они увидят отсутствие штриха, у них возникает повод поинтересоваться, почему я считаю объем газа неизменным. Если таких специалистов нет, то что-то прободное может просочиться. Если они есть, впрочем, тоже))).
Есть у меня общая проблема – я не знаю, как считать сумму любого свойства по объему, а не конкретную сумму плотностей, которая является массой. Бороться я буду именно с этой общей проблемой потому вначале заменяю конкретный буквы на абстрактные. Абстрактное свойство, размазанное по объему у меня станет букой A, а его сумма по объему I (наверное, от слова «интеграл»).
Перепишу все это с новыми буквами:
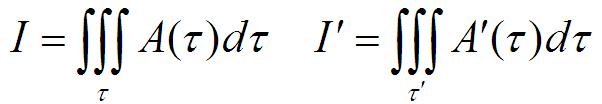
Замечательно. С первым выражением ничего не сделаешь, а со вторым можно поиграться. Например, можно добавить и сразу отнять интеграл по τ. Добавление к выражению нуля, как правило, ничего не меняет:
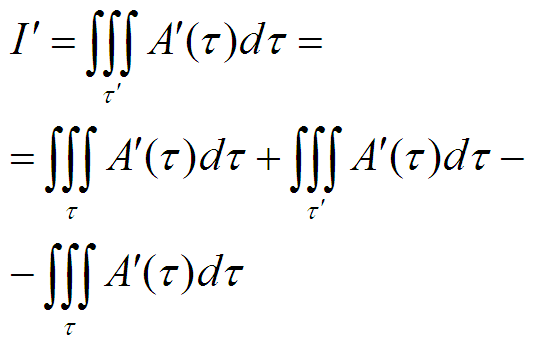
Меня, всё-таки, изменение величины суммы интересует, значит пора вычесть одно из другого:

Результат – сумма двух интегралов. В этом месте возникают ранее помянутые величины какого-то порядка малости, которые будут отброшены.
Подынтегральное выражение первого интеграла я разложу в ряд Тейлора (то, что так можно раскладывать тоже доказывается в математическом анализе):
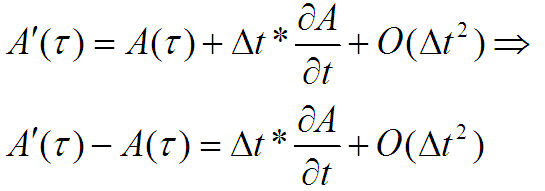
O(t2) – обозначение величины второго порядка малости. Это «О» я и отброшу. Это всё означает, что у меня тут есть малый, как всегда при дифференцировании, промежуток времени Δt. Пусть это сотая секунды. То. что я отбрасываю, т.е какое-то не астрономическое изменение плотности в отброшенном будет умножено на 0.01 дважды. Есть вклад этой величины в результат, но это порядка одной десятитысячной.
Во втором из полученных интегралов выражение интегрируется по разности объемов:
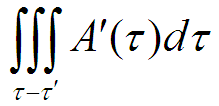
Эту разность объемов можно схематично нарисовать как кольцо:
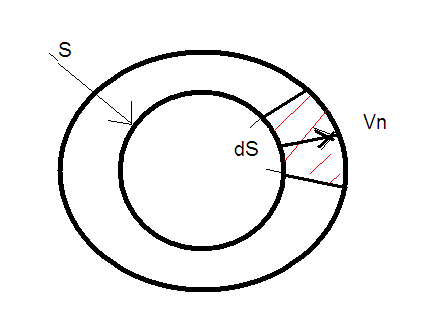
… т.е внутренний круг – это начальный объем. Газ, например, расширился и занял всё пространство большого круга. У начального объема была поверхность S. В данном случае можно перейти от интеграла по объему к интегралу по поверхности потому что заштрихованный объем можно посчитать так:
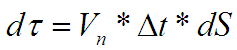
… т.е стартовая площадка dS (типа площади цилиндра) умноженная на его высоту (которая равна скорости расширения, умноженной на время расширения)/
Такой вычисление позволяет перейти от интеграла по объему к интегралу по площади поверхности:

Наверное, пора записать итоговое выражение для изменения той самой суммы свойства за период, с учетом отброшенной величины второго порядка малости и этого интеграла по поверхности:
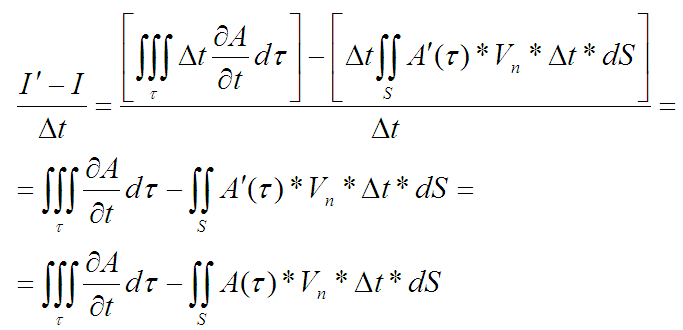
Тут довольно скользкий момент. «A» второго интеграла в последней строке потеряло штрих. Так можно сделать, потому что промежуток времени стремиться к нулю.
Самое смешное, что дальше этот интеграл по поверхности S преобразуется обратно к интегралу по объему:
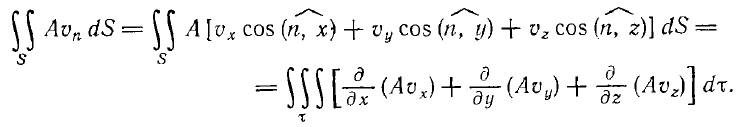
… явно по какой-то стандартной формуле из какой-нибудь дифференциальной геометрии.
Результат засовывается в искомое изменение за период:
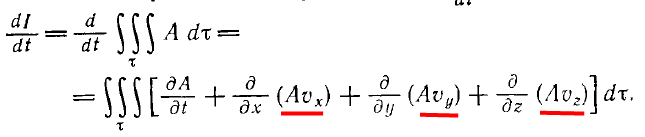
То, что подчёркнуто, дифференцируется по правилу дифференцирований произведений функций:

… после чего подынтегральное выражение расползается на две строки:
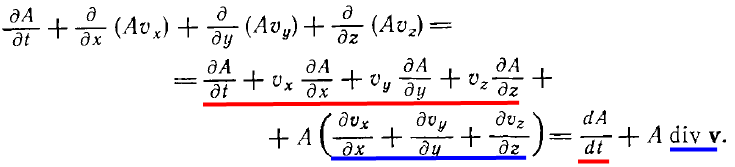
То, что подчёркнуто красным – это полный дифференциал, т.е полное изменение значения свойства, полученное в предыдущем тексте.
Самое интересное, что в начальном ошибочном варианте было получено именно это значение. И утеряно подчёркнутое синим.
Такой вариант модели, впрочем, тоже возможен. Это частный случай несжимаемой жидкости:

|









