Уравнение Лапласа
Третье уравнением математической физики называется уравнением Лапласа и выгладит так:
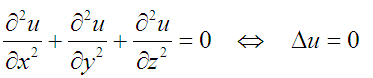
Это две записи одного и того же. Короткая справа – так называемый оператор Лапласа (означающий то, что написано слева).
Уравнения такого вида часто возникают при исследовании упругости – пластичности -прочности. А в этих задачах своя проблема. Струна это понятный одномерный объект. Двухмерные мембраны тоже обычно квадратные иди круглые. Основное что интересно когда речь идёт о тепле: сколько его вытекло через стенку. Это тоже, во многом одномерная задача.
А вот какая-нибудь железка, которую как-то растягивают, сжимают или гнут может быть любой (включая очень сложную) формы. И это тоже нереально как-то посчитать не численно.
Потому делается примерно так как было описано тут:
http://akostina76.ucoz.ru/blog/2018-03-16-4905
… т. е решение последовательно строится, взяв за базу начальные и граничные условия и заменив производные приращениями.
Здесь делается именно это:
https://youtu.be/pjqvuDnH7V4?list=PLM66dyir0u2ctKIPmSloSdk-OSklESwMF
Нарисовали сложную по форме железку, разбили на те мелкие куски, по которым будет идти расчёт и нарисовали как будут приложены силы:

Раз уж это трёхмерный объект, который крутят на экране, то и силы логично задавать щелкая мышкой по разным граням. Но на самом деле это всё то же задания функций, начальных и граничных условий. Просто в таких задачах их очень много и их другим способом даже записать сложно при реально сложной геометрии (а такая в реальности почти всегда).
Тут немного про программу:
http://lab18.ipu.ru/projects/conf2005/3/11.htm
Описанный метод называется «метод конечных элементов». Есть и другие программы, которые это делают. Но в других сразу результат и не видно как идёт разбивка на элементы:
http://www.solidworks.com/sw/resources/videos/demo-library-solidworks-simulation.htm

| 








