Вероятность результата 9:21 при 30 подбрасываниях

Домучила вчерашний пример:
http://akostina76.ucoz.ru/blog/2019-03-20-5726

Для начала: всё там правильно считалось. Я просто не учла толщину столбиков. Расчёт отклонения для примера со столбиками:
 

Т.е для 4-х подбрасываний:

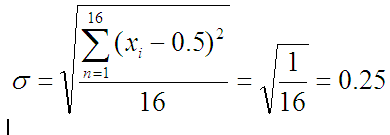
Столбики выглядят так:

Два левых столбца это 5 квадратов, т.е вероятность 5/16=0/31. Но, не смотря на такие суммы по штукам:
 

… я не могу интегрировать по первым двум строкам, т.е от 0 от 0.25 потому что второй столбик почти весь правее значений 0.25. Тут уж логичнее брать 0.25+половину до 0.50, т.е 0.25+0.125=0.375.

Вручную рассчитанная вероятность = 5/16=0.31. Похоже.
Теперь проделаю тоже самое для килобайта вариантов:

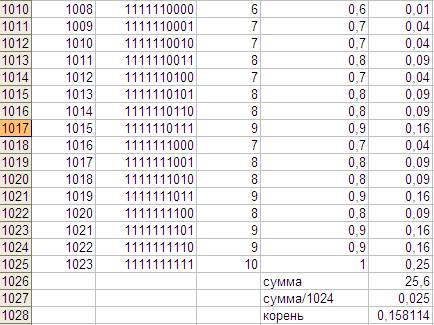
Доля единиц <=30% в 176 строках из 1024=0,171875. Это как если бы я просто вручную пересчитала крестики.
Осталось определиться с  диапазоном интегрирования. Как и в прошлом варианте это 0.3+ половина ширины столбика, т.е 0.35. Значение интеграла по этому диапазону=0.1712169716.
Инструмент – нормальное распределение для приближения квадратов гладкой функцией работает и выдаёт вполне сопоставимые результаты.
Следующий вопрос: откуда взять неизвестную дисперсию (отклонение)?
Меня интересует какая она будет при 30 подбрасываниях. Значение σ при количестве от 1 до 10 я легко могу вычислить в Excel-е.
Вот они:
 

А так это выгладит на графике:

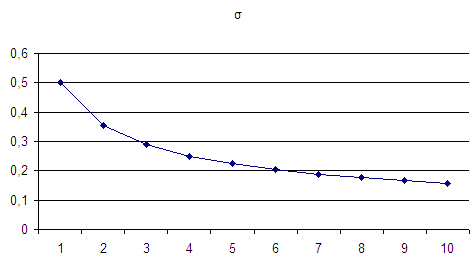
Судя по виду это явно какая-то комбинация сумм 1/x, 1/x^2 и прочего такого же.
1/x так выглядит:

Небольшой проблемой является то. что обычная интерполяция раскладывает не по отрицательным а по положительным степеням X. Если просто засунуть цифры в функцию inperp() он даже что-то посчитает, но поскольку x, x^2, x^3 и т.д явно не подходят для приближения функции такого вида, за пределами интервала от 1 до 10 начнётся ужас что (сразу на бесконечность какую-нибудь почти наверняка уйдёт).
Потому надо сделать замену переменных. Для интерполяции, т.е расчёта функции-полинома, проходящей через эти точки,  выберу три значения σ (этого оказалось вполне достаточно):

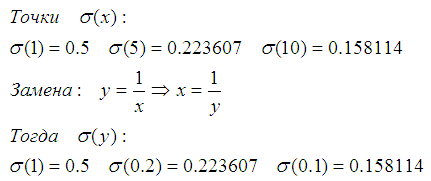
Запускаю интерполяцию:
interp([0.1,0.2,1],[0.158,0.224,0.5],y);

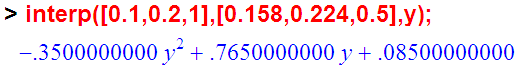
Приближающая график функция получена. Осталось сделать обратную замену переменных. Функция будет такая:

P_x := [1,2,3,4,5,6,7,8,9,10];
S_y := [0.5,0.353553391,0.288675135,0.25,0.223606798,0.204124145,0.188982237,0.176776695,0.166666667,0.158113883];
n:=nops(P_x);
fr:=[seq([P_x[i],S_y[i]],i=1..n )];
plot([fr,s],x=1..30,style=[point,line],scaling=UNCONSTRAINED, title=sigma,thickness=[3],symbol=CIRCLE,labels=[N,S],labelfont=[TIMES, BOLD, 14],titlefont=[TIMES, BOLD, 16],tickmarks=[10,5]);
Не смотря на то что для построения функции были выбраны всего три точки, приближает она совсем неплохо:

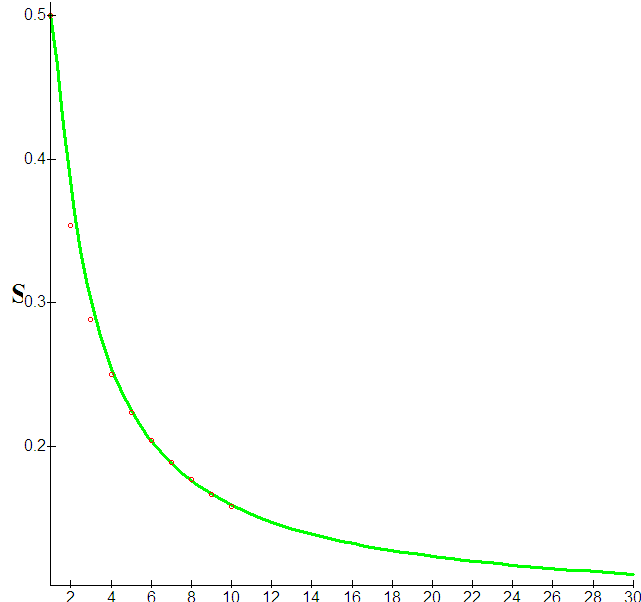
При 30 подбрасываниях значение функции σ= 0.111. Вероятность события при таком значении разброса =3.58%. Чтобы получилось 4-5% как у Кимбла надо значение 0.12. Но это не принципиально. Главное что получен результат, который выгладит обоснованным (а чего этой дисперсии не приближаться полиномом?). С какой стати она изменяется по такому закону, я не знаю, но мне пока не надо.
Это был чистая импровизация и, вообще-то, это – не метод. Как это полагается делать, узнаю, когда дальше прочитаю))).