Вывод уравнения теплопроводности
Взято тут:
http://vicaref.narod.ru/PDE/index4.htm
Выводится уравнение как обычно из закона сохранения. В данном случае это закон сохранения количества тепла. И, как часто бывает с законами сохранения, речь идёт о законе изменения, т.е изменение dQ<>0.
Выбирается некий объем материи и изучаются его температуры T, которые разные и в разных точках и в разные моменты времени, т.е T=T(x,t):

То что он цилиндрический тоже обычно для одномерных задач. А пока интересует этот одномерный случай переноса тепла из одной точки в другую через абстрактный прямой стержень.
Длина цилиндра – Δx, площадь круга – S. Свойства материала будут представлены двумя константами. Это плотность ρ и удельная теплоёмкость материала C.
Из определения этой самой теплоёмкости C:
С = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1 градус.
То же самое определение можно записать формулой, соединяющей поступившее в цилиндр тепло, внутреннюю температуру и эту константу:
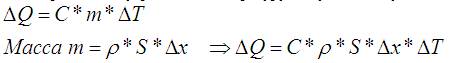
При одном кг, одном градусе Q=C, а если всё это единице не равно, оно появляется в виде коэффициентов.
Есть уравнение связи поступившего извне тепла с изменением изучаемой и искомой в данном случае температуры T.
Тепло в этой упрощённой модели входит и выходит через «крышки» цилиндра. Считается что боковая поверхность тепло не проводит (потому что это модель).
Т.е оставшаяся в объеме ΔQ вычисляется по формуле:
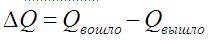
Это и есть запись уравнения сохранения -изменения количества тепла.
Вопросом интересовался Фурье и чисто экспериментально установил связь между потоком тепла через «стенку» и температурой:
https://www.calc.ru/Zakon-Furye-Osnovnoy-Zakon-Teploprovodnosti.html
Записывается полученный закон так:
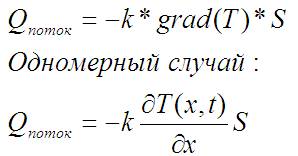
Ещё одна константа материала k – коэффициент теплопроводности ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1 градус).
Если бы всё было по 1 (и разница температур и площадь S) было бы Q_поток=-k, но тут иначе потому тоже целое уравнение.
Осталось всё это аккуратно записать и приравнять засунув в закон сохранения:
 Сократить S и все поделить на Δx и Δt: Сократить S и все поделить на Δx и Δt:

Я тут, мягко говоря, очень вольно обращаюсь с дельтами и знаками производных, но в том самом бесконечно малом случае это всё одно и то же.
Осталось перекинуть все коэффициенты в одну сторону, и поменять привычное обозначение температуры буквой T на привычное для уравнений математической физики u:
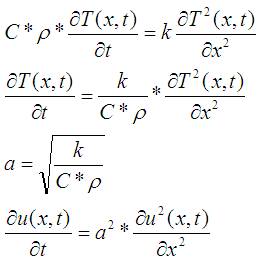
Имеет смысл выписать размерности констант.
Коэффициент теплопроводности k - Вт/(м*К)
Удельная теплоёмкость C - Дж/(кг*К)
Объемная плотность ρ – кг/м3
Параметр «теплопроводность» теплоизоляционных панелей (RockWool):
http://www.rockwool.ru/products/rockwool_standart/
λ10 = 0,036 Вт/(м·К)
… по размерности близок к коэффициенту теплопроводности k. Плотность панели 90 кг/м3. Удельная теплоёмкость 0.84 кДж/кг на 1 градус, т.е 840 Дж/(кг*К).
А что такое вот это:
λ10 = 0,035 Вт/(м·К)
λ25 = 0,037 Вт/(м·К)
λА = 0,038 Вт/(м·К)
λБ = 0,040 Вт/(м·К)
… ещё надо выяснить. Видимо они в этот параметр как-то засунули толщину стенки.
|









