Задача о дегустаторах вин
Есть мнение, что вино из бутылки открытой полчаса назад вкуснее, чем из бутылки, которую открыли только что. Решили это проверить, провели два разных по методу исследования. Получили два разных ответа.
С механико- математической точки зрения это явный признак того, что оба ответа неправильные. Потому что существует всё то же определение корректно поставленной задачи. Пока не доказали, что решение будет одно и решать не надо, надо разбираться с постановкой задачи. Проблема только в том, что в механике ещё что-то можно выцарапать с помощью математических выкладок, т.е доказать ту самую корректность задачи.
Здесь же нет таких критериев. Потому все задачи и требуют индивидуального подхода, изучения всё-таки наборов данных (во многих спорных случаях) и мысленного диалога собственных представлений (типа нулевой гипотезы) с посчитанным результатом. Тут нет точных ответов (только их вероятность). И даже точный и весьма вероятный ответ оставляет возможность усомниться (если есть какая-то внутренняя уверенность).
Вот такая интересная специфика. Пример с винами по форме похож на подгонку результатов под начальное представление. С другой стороны выводы в нем обоснованы. И сделаны они при изучении внешнего вида выборки, хотя обычная цель статистики как раз избавить человека от созерцания графика и дать ему одну точную цифру.
В первом случае взяли 20 человек, половине дали попробовать вино из только что открытой бутылки, а половине – из открытой полчаса назад. Оценки качества вин в таком эксперименте:
|
Дегустатор
|
Оценка для только что открытого
|
Оценка для открытого 30 минут назад
|
Разность средней оценки
|
|
1
|
16
|
16
|
|
|
2
|
9,5
|
12
|
|
|
3
|
15
|
15,5
|
|
|
4
|
15,5
|
15
|
|
|
5
|
13
|
14
|
|
|
6
|
16,5
|
18,5
|
|
|
7
|
14,5
|
18
|
|
|
8
|
17
|
13
|
|
|
9
|
12
|
17,5
|
|
|
10
|
17,5
|
17
|
|
|
avg
|
14,65
|
15,65
|
1
|
|
S+
|
2,494995
|
2,173707
|
|
|
S_M
|
0,788987
|
0,687386
|
|

Оценка для вина открытого позже обычно выше. Ожидаемо. Но совершенно непонятно почему так сильно вверх и вниз прыгают цифры. Точнее это-то означает, что люди – не физические приборы, кто-то привычно ставит оценки чуть выше, а кто-то ниже. А вот почему оценки прыгают синхронно (т.е велика корреляция выборок) не понятно вообще и совсем. Может там где пил второй человек окружающий вид какой-то некрасивый?
Получена разница средней оценки в 1 балл. Но большой разброс значений (что-то типа погрешности измерения) больше двух баллов. В таком большом разбросе, который станет «широкой горкой» различие, даже если оно есть, закономерно потеряется. Ведь t-оценка просто посчитает пересечение широких горок:
https://akostina76.ucoz.ru/blog/2019-04-13-5779
Ни в каком учебнике не описать, что надо делать при получении такого набора данных. Можно разве что сказать, что большой разброс – тревожный симптом, при котором разное может быть названо одинаковым. Надо от ней избавляться если есть такая возможность.
Это и было сделано. Во втором эксперименте одни и те же люди пили вначале вино из только что открытой бутылки а потом его же но «подышавшее». Ставили оценки. Результат такой:
|
Дегустатор
|
Оценка для только что открытого
|
Оценка для открытого 30 минут назад
|
Разность оценки
|
|
1
|
17
|
18,5
|
1,5
|
|
2
|
17,5
|
18
|
0,5
|
|
3
|
16
|
17,5
|
1,5
|
|
4
|
16,5
|
17
|
0,5
|
|
5
|
15,5
|
16
|
0,5
|
|
6
|
15
|
15,5
|
0,5
|
|
7
|
14,5
|
15
|
0,5
|
|
8
|
13
|
14
|
1
|
|
9
|
12
|
13
|
1
|
|
10
|
9,5
|
12
|
2,5
|
|
avg
|
14,65
|
15,65
|
1
|
|
S+
|
2,494995
|
2,173707
|
0,666667
|
|
S_M
|
0,788987
|
0,687386
|
0,210819
|
На графике так:
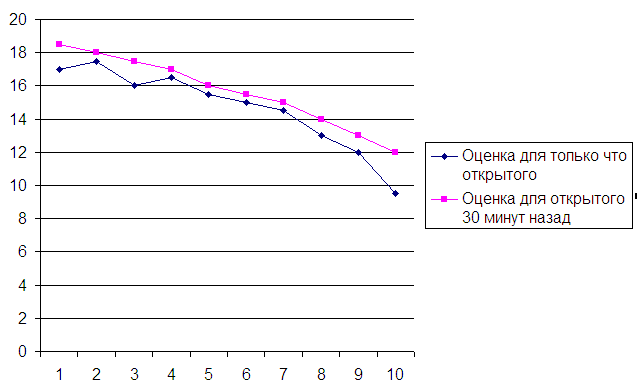
Корреляция не пропала, скорее сильнее стала (но теперь у неё есть понятная причина – отличие людей). Всё то же отличие средних оценок в 1 балл на графике стало более выраженным. Других вариантов нет, разве что можно предположить, что дегустаторы знают об эффекте улучшения качества и предполагают, что проверяется именно это (отсюда такие дружно лучшие оценки).
Вообще-то такое однообразие результата – тоже повод усомниться в достоверности.
Зато такой эксперимент позволяет исследовать не два столбца дынных, а один с их разностью (справа).
Для этой разности можно посчитать всё то же самое и проверить вероятность полученного среднего значения по Z-оценке.
Горка распределения в данном случае имеет вершину в нуле. Ведь предполагается что нет никаких отличий в оценках (т.е разность равна нулю), а требуется узнать можно ли считать статистической погрешностью отличие в 1 балл. Т.е требуется узнать вероятность того, что это отличие случайно.
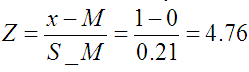
Если верить методу эксперимента и расчёту так вообще не может быть. Никогда. Z должно быть между -3 и 3 в хоть сколько-нибудь вероятных случаях. В таблице такого нет, но посчитанная по интегралу вероятность =0.9589*10^(-6).
Интересно сравнить с результатом по t-оценке по двум наборам с учетом корреляции (равной 0.97):
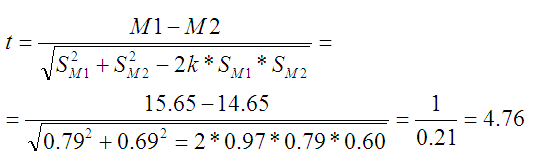
Результаты подозрительно совпали. Видимо на то есть какие-то веские причины))). Теперь полагается обращаться к таблице для t-значений, хотя сам вид функции – полный аналог вычисления Z-оценки. Там явно то же нормальное распределение. Только дисперсия как-то хитро вычислена.
Интересно, что t-оценка даёт вероятность в 1000 раз больше:
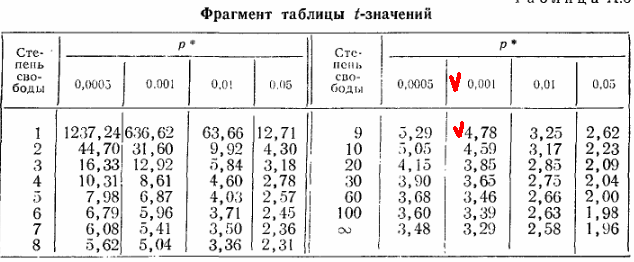
… т.е по ней проще посчитать разное одинаковым (вроде бы).
Просто интересно как факт, как свойство измерительного инструмента. Строго говоря, не важно чем измерять, наверное. Всё равно ведь сравниваться будут меньшие (более вероятные) и большие (менее вероятные) значения Z и t. Но их отличиям не стоит удивляться. Здесь так бывает))).
Интересно подвести некоторый итог. В статистике, похоже нет математически точной информации. Есть число и «облако» вокруг него. Здесь с такими объектами принято иметь дело. А описанный выше метод позволяет определить, можно ли считать небольшое отклонение например, от нуля всё ещё нулём. Или это действительно уже другая цифра (и другой объект или ситуация) а не погрешность измерительного прибора.
|









