Закон количества движения
Внимательно смотрю на эту парочку уравнений из погодной системы:

Они задают соотношение давления (p) и проекций скорости на оси (на ось X – U, на ость Y – V). Вспоминаю, что давление – это почти сила (давление это сила делённая на площадь её приложения). А скорость это почти ускорение (точнее ускорение это отношение изменения скорости к изменению времени, что и присутствует в левых частях этих уравнений).
Компания из силы и ускорения заставляет вспомнить второй закон Ньютона (сила равна массе, умноженной на ускорение). Эти уравнения – он и есть.
Осталось их аккуратно вывести для общего случая любых сил, приложенных к любому объему жидкости или газа.
Пусть есть какой-то объем жидкости или газа. На него явно может действовать два вида сил. Это – массовые силы, приложенные к каждой молекуле изучаемого вещества и поверхностные силы, т.е силы, которые давят на это кусок среды с боков.
Стандартный пример массовых сил – сила тяжести. Каждая молекула среды притягивается к земле.
В уравнениях есть параметр «l» - параметр Кориолиса. Эта сила связана с вращением Земли. Не важно, что там куда направленно. Важно, что это тоже явно массовая сила также как какая-нибудь центробежная сила.
А давление оно просто по определению давит сбоку. С какой стороны давит меньше, туда и летит воздух. Это – поверхностная силы.
Теперь всё то же самое аккуратно:

Из-за гипотезы сплошной среды тут всё достаточно гладкое для того чтобы вначале заявить о существовании средней массовой силы по объему, потом перейти к функции силы, какое-то значение которой есть во всех точках пространства в любой момент времени ( F(z,y,,z,t) ). После этого можно интегралом просуммировать все силы, которые действуют на объем. Поскольку действуют они, всё-таки не на объем, а на массу (которая равна произведению плотности на объем), под интеграл попала и плотность ρ.
Про поверхностные силы всё то же самое:

… но, поскольку суммируютcя силы по поверхности, итоговый интеграл тоже по поверхности S.
Не помню термина «количество движения». С другой стороны, наверное, интуитивно понятно, что это. И интуиция, в общем, не обманывает. Это – сумма скоростей всего, что движется в объеме:

Здесь появляется скорость «v» и умножается на массу (вообще-то, это импульс, но это не важно). Масса, как обычно это плотность, умноженная на объем, потому плотность под интегралом, а объем это сам интеграл.
Дальше формулируется закон, утверждающий, что все изменения в движении вызваны какими-то силами:

Если вместо букв подставить интегралы, то закон перепишется так:

Здесь:
https://akostina76.ucoz.ru/blog/2020-08-04-6663
… выводилась формула для закона сохранении массы. Но весь вывод вместо плотности ρ писалось «A», означающее любую функцию.
Слева в формуле изменение количества движения. В роли «A» тут произведение плотности на скорость. Ничего не мешает использовать для этого выражения уже полученную формулу и получить такое:

В формуле закона два интеграла по объему и один по площади. Интегралы по объему можно объединить:
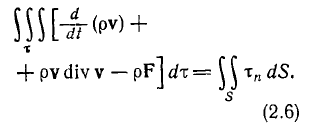
А интеграл по площади можно перевести в интеграл по объему по формуле, как оказалось, Гаусса – Остроградского:

Я писала, что это явно какая-то стандартная формула. Оказалось, что у формулы даже фамилия есть.
Теперь всё можно засунуть в один интеграл по поверхности и выкинуть интеграл:

… потому что равенство нулю интеграла по любому объему может быть только при равенстве нулю подынтегральной функции.
Продифференцировав первое слагаемое по стандартной формуле и немного поиграв скобками, можно получить такое:
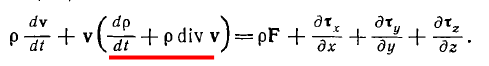
Подчёркнутое равно нулю по закону сохранения массы, это – формулировка того закона.
Значит, всё это переписывается в таком виде:
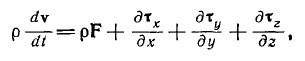
Осталось вспомнить, что скорость v – вектор, т.е это три составляющие, три цифры проекцией на оси X, Y. Z. Значит, тут написано не одно уравнение, а сразу три. Если всё поделить на плотность, то получится так:

Это – самая общая формула, для всех жидкостей, включая вязкие, т.е такие, в которых надо учитывать касательные напряжения. Если нет необходимости учитывать вязкость, то от 9 функцией остаётся только то, что по горизонтали (подчёркнутое красным). Остальное равно нулю. А в случае атмосферы в погодной задаче – единственная поверхностная сила – давление p. Оно и присутствует в формуле.
|









