Эксперименты и функции

Здесь было про спиртовые дрожжи:
https://akostina76.ucoz.ru/blog/2020-09-04-6722

… на упаковке которых написано так:

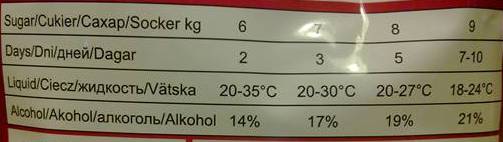
Производительность дрожжевого труда в молях в час меня сейчас не интересует. Также как и условия, при которых так должно быть.
Пусть кто-то взял эти дрожи и нужное количество сахара, провёл 4 эксперимента и получил такие результаты.
Я могу их нарисовать на плоскости, где по оси X – количество дней, а по оси Y – градус. Будет так:

Но меня-то, скорее всего, интересует не это, а можно ли с помощью этих дрожжей получить 40 градусов. А если можно, то когда. Задача науки не только фиксировать, но и предсказывать.
Проблема в том. что пока я не предположу, по какому закону изменяются эти данные, я ничего не смогу предположить. Мне надо предположить какую-то функцию y=y(x). И предположить, что часть уже полученных точек – экспериментальных данных – это точки этой функции.
В данном случае градус явно увеличивается со временем. Мне никто не мешает, предположить, что здесь линейная зависимость, т.е то, что эти точки лежат на прямой линии. Не лежат они на линии? А может это из-за погрешности измерений.
Запущу метод наименьших квадратов и получу линию:
day_x := [2,3,5,10];
Grad_y := [14,17,19,21];
n:=nops(day_x);
b1:=(add(Grad_y[i],i=1..n)*add(day_x[i]^2,i=1..n)-add(day_x[i],i=1..n)*add(day_x[i]*Grad_y[i],i=1..n) )/(n*add(day_x[i]^2,i=1..n)-add(day_x[i],i=1..n)^2);
k1:=(n*add(day_x[i]*Grad_y[i],i=1..n)-add(Grad_y[i],i=1..n)*add(day_x[i],i=1..n))/(n*add(day_x[i]^2,i=1..n)-add(day_x[i],i=1..n)^2);
fr:=[seq([day_x[i],Grad_y [i]],i=1..n )];
plot([fr,b1+x*k1],x=0..30,style=[point,line],scaling=UNCONSTRAINED, title=grad,thickness=[3],symbol=CIRCLE,labels=[day,grad],labelfont=[TIMES, BOLD, 14],titlefont=[TIMES, BOLD, 16],tickmarks=[10,5]);

… показывающую, что 40 градусов я получу через месяц.
Но точки действительно не очень лежат на прямой. Я могу улучшить ситуацию, оставив только две точки по известной шутке «если по результатам эксперимента надо получить прямую, получайте её по двум точкам». По двум точкам всегда можно построить прямую, причём единственную (как по трём точкам единственную плоскость).
Но «улучшать» ситуацию я буду не так, а с помощью интерполяции полиномами т.е функциями x^N, с помощью которых можно получить не только прямую,  а что угодно как угодно изогнутое.
Вот такой полином хорошо приблизит эти точки:

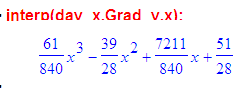
day_x := [2,3,5,10];
Grad_y := [14,17,19,21];
n:=nops(day_x);
fr:=[seq([day_x[i],Grad_y [i]],i=1..n )];
plot([fr,interp(day_x,Grad_y,x)],x=0..19,style=[point,line],scaling=UNCONSTRAINED, title=grad,thickness=[3],symbol=CIRCLE,labels=[day,grad],labelfont=[TIMES, BOLD, 14],titlefont=[TIMES, BOLD, 16],tickmarks=[10,5]);
А при таком приближении получится, что я аж 150 градусов получу через 19 дней:

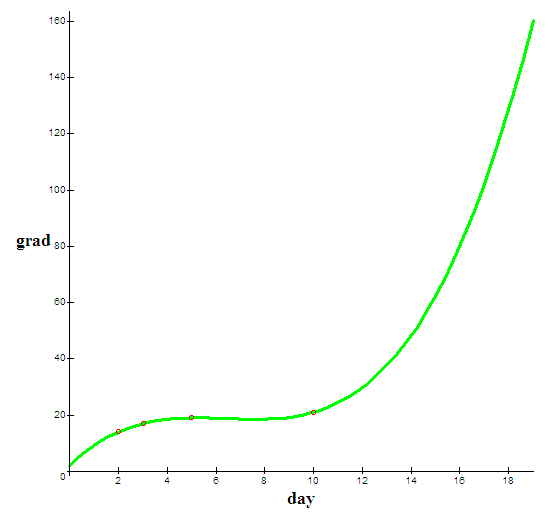
Происходящее вызвано тем, что вид функции лучше брать с известных законов (или самостоятельно придуманных, но как-то обоснованных). По ним пишутся дифференциальные уравнения, позволяющие получить примерный вид функции. А если таких нет, то надо лучше угадывать этот вид функции. Все полиномы при X=бесконечность бесконечны, чего в этой задаче явно не может быть. Но в случае угадывания предсказательная способность этой деятельности уже висит в воздухе. Хотя никто не мешает сделать и так, т.е предположить вид по небольшому количеству информации, а потом расширить диапазон проверки. Если за пределами диапазона точки тоже будут лежать на функции, которую просто предположили, наверное так оно и есть (т.е функция угадана правильно).
Расположение точек похоже, скорее, на такую функцию:

… и заставляет предположить, что приближать надо иксом в степени половина, треть и т.д.
Примерно также, как это было сделано здесь:
https://akostina76.ucoz.ru/blog/2019-03-21-5728
… можно ввести замену переменной… и получить какую-то бредятину… Вид графика тот, но не больше 14 градусов))).
Не важно. Главное тут то, что все предположения, включая вид приближающей функции, должны быть как-то обоснованы.

А что касается реального процента спирта… всё-таки требуется более детальное исследование происходящего с моделью поведения дрожжей при разной концентрации спирта и сахара))). Интерполяцией что угодно подучить можно, но дрожжи в математике не разбираются, потому не в курсе.