Учёт наклона земной оси

Что-то мне говорит, что я не смогу остаться в плоской системе координат. После этого события:
https://akostina76.ucoz.ru/blog/2020-12-22-6873

… возникло желание узнать, как рассчитать высоту Солнца над горизонтом (явный угол плоскости к координате Z) и азимут, т.е направление на восток, юг, запад (точнее угол в плоскости земной поверхности).
Но вначале имеет смысл аккуратно записать полученный тут:
https://akostina76.ucoz.ru/blog/2021-01-01-6891

… результат.
Например, так:

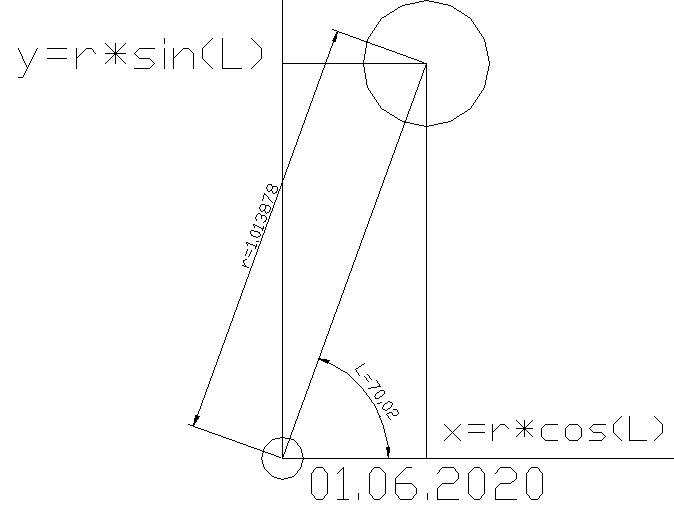
Здесь показано взаимное расположение Земли  и Солнца 1 июня 2020 года. Угол в полярной системе координат (долгота Солнца) равен 70 градусам. А расстояние r от Солнца до Земли – астрономическая единица с какими-то «копейками».
Кроме полярной можно нарисовать и обычную прямоугольную систему координат X, Y.  И даже рассчитать координаты в этой системе координат по известным значениям радиуса и угла.
Трёхмерная система координат из двухмерной делается легко и просто. Добавлением оси Z и присвоением её нуля, ведь пока ничто не вышло за пределы плоскости:
x=r*cos(L)
y=r*sin(L)
z=0
Картинка поменяется на такую:

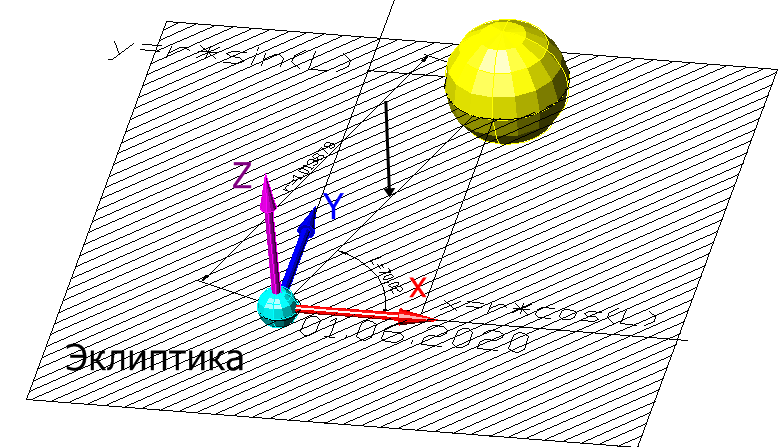
Ось X тут показана красной стрелкой, ось Y – синей, а добавленная ось Z – малиновой. Направление на солнце в этой системе координат продолжает лежать в заштрихованной плоскости, потому z=0.
А теперь я хочу учесть то, что земная ось наклонена примерно на 23 градуса. Точная формула расчёта этого угла такая:
oblecl = 23,4393 - 0,0000003563* d
Я нахожусь на Земле. Меня интересуют мои ощущения, т.е под какими углами я буду видеть Солнце. Почти наверняка мне проще будет, если я сразу поверну оси координат так, чтобы направление Z совпадало с направлением оси вращения. Крутить мне придётся на угол 23 градуса вокруг оси X. Для пересчёта в новую систему координат (т.е повернутую относительно исходной) есть набор формул. Только надо аккуратнее с направлением углов.
Классический вид сферической системы координат:
https://ru.wikipedia.org/wiki/Сферическая_система_координат

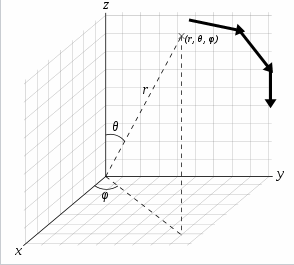
Положительный угол поворота вокруг оси X наверное будет в положительную сторону Y.
Формулы поворотов вокруг различных осей:
https://ru.wikipedia.org/wiki/Матрица_поворота

Меня из них интересует первая, т.е поворот вокруг оси X. Про матричную форму записи было тут:
https://akostina76.ucoz.ru/blog/2020-08-26-6700

… т.е всё это можно переписать в виде таких формул преобразования:


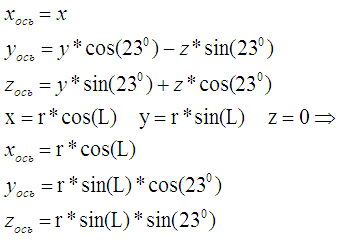
При такой замене координат, картинка меняется на такую:

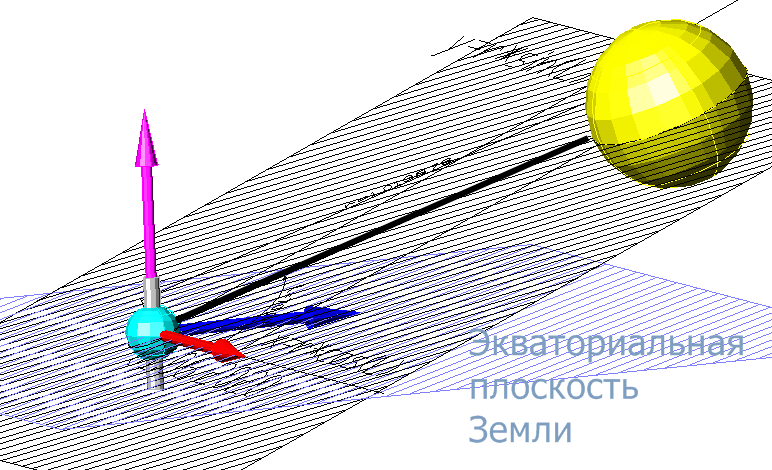
Новая плоскость X, Y лежит в том. что называется «Экваториальная плоскость Земли». А направление на Солнце получило не нулевую координату Z.
Обращаю внимание на то, что расстояние от Земли до Солнца r вроде бы во всех формулах есть, но как-то оно нигде никакой роли не играет и вообще почти равно единице. И это никому и ничему не мешает. Меня мало интересуют расстояния. Меня интересуют углы, т.е выше, ниже, правее или левее. Именно эти углы поменялись при переходе к другой системе координат. А раз меня расстояния не интересуют, уместен переход к тому, что называется «Небесная Сфера». Вообще-то вокруг меня бесконечный космос, но если я вижу только углы, то всё, что там происходит можно представить на шарике в километре от меня:

Солнце далеко, а точка на воображаемой сфере близко. Но градусные координаты у Солнца и этой токи одни и те же. Если меня интересуют только градусы, а вполне могу заменить одно другим и в голове и в вычислениях.
Точно также на эту воображаемую небесную сферу проецируются и все остальные объекты вселенной.
При всех видах вращения (и вокруг Солнца и вокруг своей оси) ось Z направлена на северный полюс и в определённую часть космоса.
А там находится Полярная Звезда, вокруг которой «вращается» Малая Медведица:

Полный оборот совершается за 24 часа:

Вращается, конечно, не Медведица, а Земля, не меняя при этим вращении ориентировки северного полюса на эта часть вселенной и Полярную звезду. По положению «ковша» можно приблизительно определить время.