От конечных элементов до механизмов

Конечный элемент это такой очень маленький кубик, на который воздействуют соседние маленькие кубики.
Я думала, что Зенит-95 это программа для расчёта напряжений, деформаций и прочности. Я ошибалась. Вначале они туда засунули всю математическую физику. Потом добавили теоретическую механику. После этого добавление механизмов, т.е комбинаций сред, на которые действует не только закон всемирного тяготения в виде силы тяжести, но и что-то рукотворное, было уже совсем небольшим шагом.
Но всё по порядку. Начиналось всё явно с прочности. Не от хорошей жизни. Написать формулы можно для струны и стержня. Надорвавши задницу, можно что-то изобразить для пластинки с круглой дыркой. Но это уже предел.
А в реальной жизни напрягается и деформируется что-то примерно такое:

… которое в аналитическом виде (формулами) обсчитать невозможно. Чего делать?
Решение сидело в тех же формулах, точнее в методе дифференциального и интегрального исчисления. Метод возник, когда не знаю кто придумал понятие «скорость» как результат деления бесконечно малого отрезка пути к бесконечно малому промежутку времени. С этого момента во всей механике сидели эти бесконечно малые отрезки и объемы.
Отсюда:
http://akostina76.ucoz.ru/blog/2017-02-09-3836
… симпатичный бесконечно малый кусочек струны, который не только переместился в пространстве про действием силы F, но и чуть-чуть растянулся:

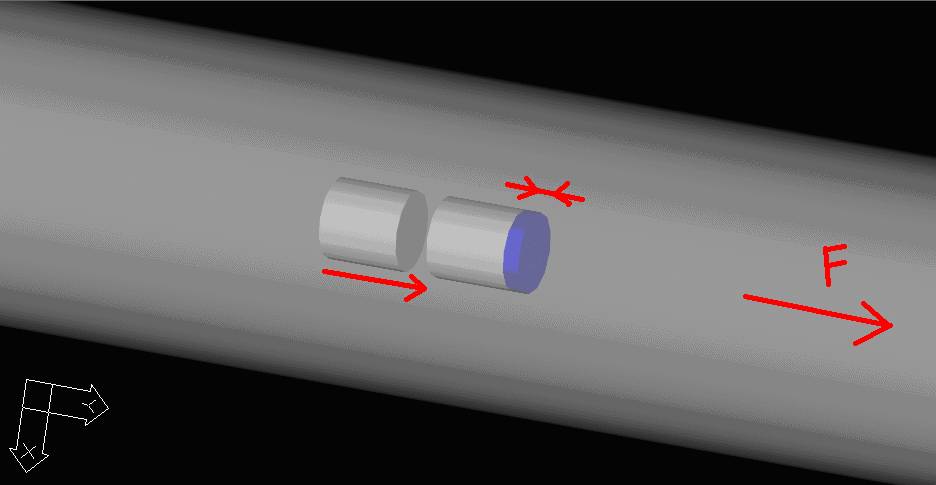
Картинка взята из вывода волнового уравнения. Все три уравнения математической физики рассматривают такие бесконечно малые кусочки и то, что с ними происходит. В волновом уравнении кусочки перемещаются и деформируются. В уравнении теплопроводности они из внешнего мира получают не растягивающие или сжимающие воздействия, а тепло. И меняют другой свой параметр – температуру.
У таких кусочков есть куча меняющихся свойств (температура, координата в пространстве, форма). А есть постоянные типа плотности, модуля упругости и т.д.
Волновое уравнение для перемещения точки струны или стержня во времени u(x,t):

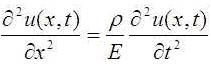
Уравнение теплопроводности для температуры T(x,t):

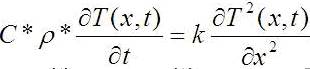
Если бы на обоях были такие рисунки, мало кто заметил бы разницу. И не зря. Можно было написать одну переменную S(x,t) от русского слова «свойство» (вместо разных u(x,t) и T(x,t)), потому что результат решения – информация о свойстве маленького кубика в точке с координатой x. Мало ли какие бывают меняющиеся свойства. Ещё в уравнениях есть компания констант материалов (k,р,C). От этих констант зависит значение функции, т.е ответ задачи, т.е величина искомого свойства.
Короче, это два дифференциальных уравнения, на которые напускается некий математический аппарат, который о физической природе процессов вообще ничего не знает, потому для него это тоже совершенно одинаковые  «обои».
Я пытаюсь рассказать про объемные кубики, в основном, всё-таки деформируемые. Но поскольку математический инструментарий везде одинаков я заменю перемещения температурами и приведу в качестве простого примера численное решение уравнения теплопроводности:
https://akostina76.ucoz.ru/blog/2020-09-24-6767

В этом расчете у меня нет ни только трёхмерных кубиков, но и даже двухмерных квадратиков. У меня пространственная координата X и время t.
Чтобы посчитать значения в следующей точке и в следующий момент времени, я использую значения в соседних (по координате или времени точках):

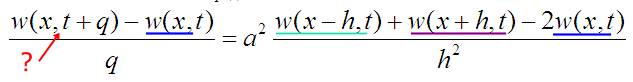
Считать я по этой формуле буду температуру, обозначенную на этот раз безликой буковой w. А зависит она от температуры, которая была в этой точке в предыдущий момент времени (w(x,t)) и температур, которые были в соседних точках ( w(x-h,t) и w(x+h,t)). Все эти температуры как-то передаются и смешиваются.
Точно также в деформируемой железке маленькому кусочку передаются воздействия соседних кусочков. Они его перемещают и деформируют. А потом уже он перемещает и деформирует следующий маленький объем.
У этого процесса должно быть начало. Точнее, начала. Если речь о нагревающейся стенке, то в начальный момент времени должны быть заданы температуры с разных сторон стенки. А поскольку всё происходит в пространстве, то надо задать ещё и толщину стенки, точнее границы пространства и то, что происходит на них. Условия в начальный момент времени – начальные условия. Условия на границах – граничные условия. Это все – обязательные части задач с дифференциальными уравнениями.
В трёхмерном пространстве, т.е когда не одна пространственная координата X, а полный набор X,Y, Z все тоже самое, только длиннее.
Бесконечно малые объемы – математическая абстракция. Для расчета мне такого тоже не надо. Для расчета мне надо чтобы кубики описывали конкретную сложную фигуру:

На сложной фигуре и показывать сложно. И продеформировать ей сложно. Уж очень она прочная)).
Потому для примера тонкая пластинка:

Слева она закреплена, а справа к ней приложена сила. Почему вверх? Потому что перепутала знак нагрузки, а корректировать мне был лень))).
Вот так эта штука продеформировалась:

Тут важно то, что кусок №2 уже ничего не знает про приложенную на границе куска №1 силу:

Для него и последующих граничным условием становится то, что твориться на соседнем участке. Так последовательно и идёт расчёт.
Но раз все эти кубики позволяет рассчитывать перемещения, то чем хуже передающаяся температура?
Потому с помощью лёгкого движения ползунка вниз можно добраться до граничных условий по температуре:

вот они в том же списке:

А уже неточное пояснение «НАГРУЗКИ» они просто забыли убрать.
С математической физикой всё.   Но ведь можно пойти и дальше. Пусть с горки катится колесо:

Задача та же – узнать какие там нагрузки и как оно деформируется. Колесо, как тут и полагается из маленьких конечных элементов. Одна проблема – колесо движется и потому силы, действующие на его элементы, постоянно меняются.
Это не очень большая проблема. Не так сложно посчитать положение колеса в какой-то момент времени на горке с каким-то уклоном и какой конкретно участок, какую нагрузку получает. Это уже относится к предмету Теоретическая механика. Но это все начали считать задолго до получения решений уравнений математической физики.
Ещё одно расширение чисто вычислительное. У меня отдельные маленькие кусочки. Ничто не мешает мне задать для каждого из них свои константы, соединив в модели железную арматуру (с характеристиками железа) и бетон (с характеристиками бетона).
Но можно пойти и дальше. Почему не залить в бак воду, чтобы узнать как продеформируются стенки бака под её весом? Можно пойти ещё дальше (гибкость вычислительного инструмента с кубиками с разными свойствами это позволяет) и добраться до предмета под названием «гидроупругость». В аэродинамике считается, что крыло самолёта не деформируется. А в теории упругости нужны постоянные силы (сила потока воздуха, например). Оба предмета – теория. На практике крылья деформируются и силы потоков меняются. С самолётами ещё куда ни шло, они жёсткие. А сосуды, по которым течёт кровь, сильно растягиваются. Исхитриться и получить формулу можно и там:
https://akostina76.ucoz.ru/blog/2020-02-16-6308

… но в численном расчёте с кубиками все совсем просто. У кубика крови есть соседи. Соседний кубик крови давил сильнее стенки сосуда, результат – перемещение туда, где был сосуд.
Но раз уже есть какие-то кубики разных элементов и сред, то можно вообще что угодно нарисовать. И пусть это все как-то воздействует на соседние участки, перемещая их.
Гидропривод из примеров:


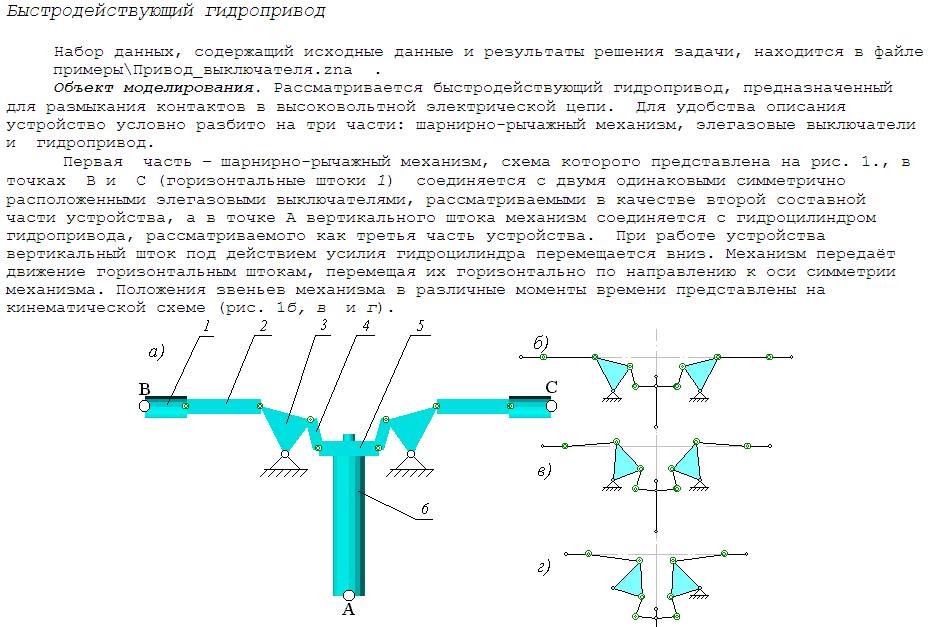
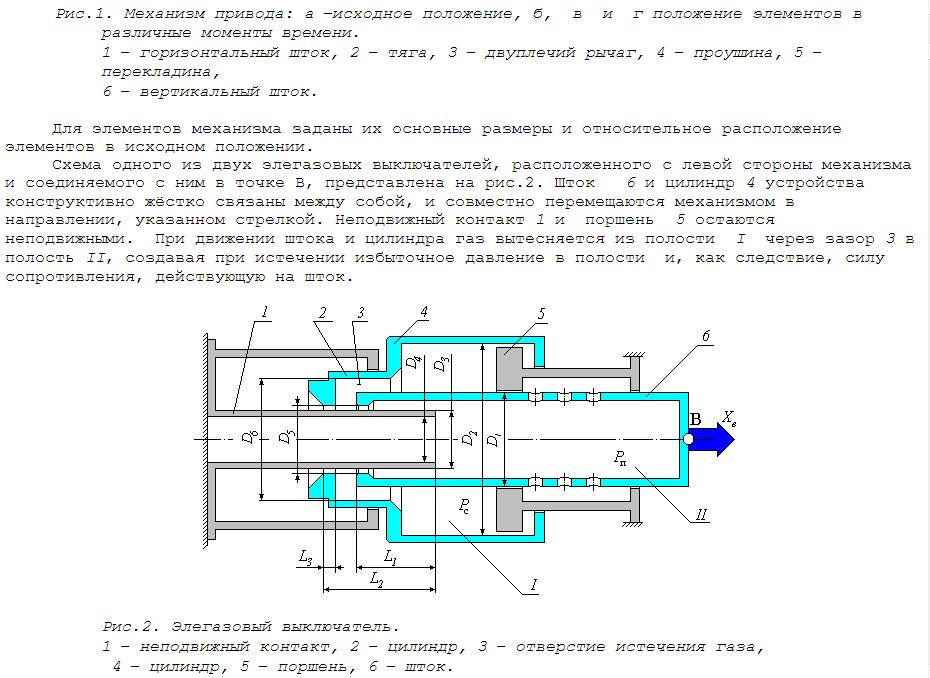
Что-то кошмарное с отдельно движущимся поршнем и всем остальным. Потому что если есть отдельная движущаяся вода, почему не завести движущейся и давящий на что-то поршень? Просто соседний элемент получит ещё одно воздействие. Так же как кусок катящегося колеса получает перемещение не только из-за деформация, но и из-за движения колеса целиком.
Вот такой программный продукт. Но мои запросы сейчас несколько скромнее его возможностей)).