Аэродинамические результаты и выводы

Такое не летит:
https://youtu.be/fHxFz0TU60o

Использование: 3 двигается 4.2V 14*6мм. Питание – 3 батарейки АА. Винт: длина – 48 мм, ширина – 8мм, толщина – 1мм, профиль – пластина, угол атаки – 5 градусов. Общий вес – 8 грамм (в т.ч рама – 5 грамм).
1] Батарейки подключены напрямую. Так и не удалось выжать через транзистор больше 2 вольт. Два двигателя ещё можно было цеплять через два маломощных транзистора. Возиться сейчас с четырьмя по той же схеме мне лень. Надо пока цеплять из всех к одному мощному. Тем более что мощный транзистор уже найден. Должно подойти, например, то, что использовано тут:
http://akostina76.ucoz.ru/blog/2018-12-08-5538

… т.е 2T809A или BD677.
2] Придуманный крепёж двигателя никуда не годится. На видео у меня нет одного, т.к он сломан. Сейчас у меня сломанных уже три. Оторвались провода:

Я была не готова использовать для закрепления силу трения, хотя в случае винта уже пришлось сделать именно это. Потому у меня там нечто сложное из суженного сверху цилиндра и отдельного дна снизу. Видимо при вставке дна оно может попасть на провод (хотя там сделана специальная прорезь). А когда сверху с усилием надевается винт, там что-то совсем сжимается, перетирается и ломается. Крепёж, похоже надо делать монолитным с той же прорезью снизу (наверное, она должны быть шире) и достаточно узким чтобы двигатель держался на трении.
Скорее всего,  имеет смысл как-то дополнительно закрепить провода к раме (чтобы не оторвать, если случайно дёрнуть).
3] Дырка в винте – 1.15мм – 1.2мм. Сказать точнее не возьмусь из-за того что формально одинаковые при печати получаются разными. Но 1.15 при необходимости расширяется булавкой, 1.2 можно сузить «ниткой».
Чтобы было понятно сколько раз это всё печаталось:

Всё выкидывать.
4] Результат не похож на то, что получено тут:
http://akostina76.ucoz.ru/blog/2018-12-11-5542

На поверхности то, что исследуемый объект вовсе не похож на бесконечно тонкую пластинку:

Бесконечно тонкая пластина это линия, не имеющая толщины. Или пластина, у которой велико отношение «a» к «h». Здесь же оно меньше 10 (точнее 8). Это не столько линия сколько слегка продеформированный квадрат, обдуваемый потоком воздуха.
Из-за большой толщины «h» нельзя пренебрегать его лобовым сопротивлением. Тем более что с уменьшением угла α эта поверхность становится той самой вертикальной стенкой, сопротивление которой максимально:
http://akostina76.ucoz.ru/blog/2018-12-07-5537

Это пусть и небольшая, но константа. Скругление и ошкуривание тут ничего принципиально не поменяет.
Малые углы особо привлекательны в этой модели из-за того, малые силы отличаются там на порядок. Подъемная сила Ry там ноль первого порядка, т.е. просто ноль (sin(0)*cos(0)=0*1).
А лобовое сопротивление  Rx там – ноль второго порядка, т.е ноль в квадрате (sin(0)*sin(0)=0*0).
Получается что как бы мала ни была подъемная сила, именно там она становится бесконечно больше лобового сопротивления.
Если на всём диапазоне углов (от 0 до 90 градусов) это выгладит так:

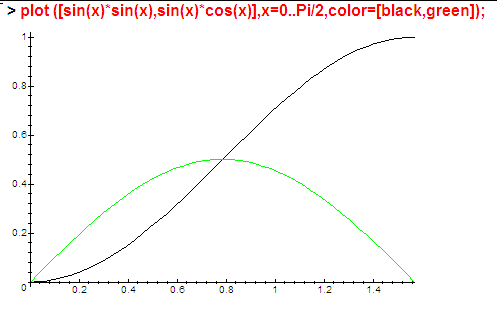
… т.е величина отличаются в несколько раз, то в диапазоне от 0 до 1 градуса:

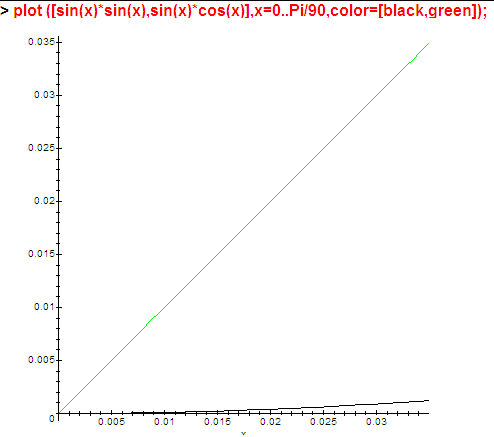
… соотношение величин совсем другое.
И это всё из-за нулевого лобового сопротивления, которого нет у бесконечно тонкой пластинки в её модели.
А у лопасти, которая у меня на двигателе это небольшое h есть. И потому там, для начала, точно нет нулевой силы сопротивления возле нуля. Этому, пусть небольшому h (и вызываемому им сопротивлению) надо перевешивать убывающей за счёт угла α ноль подъемной силы. Любая константа большая нуля перетянет ноль первого порядка. А в моём случае «h» даже не на много меньше «a».  
Потому поведение реального объекта принципиально отличается от модели (где в модели рост эффективности, там реально его нет, т.е функция имеет другой вид). Принципиально другое соотношение параметров делает модель неприменимой в этой ситуации.