Численное решение уравнения теплопроводности
Использовалось оно тут:
https://akostina76.ucoz.ru/blog/2020-09-20-6760
А сегодня я хочу показать, насколько там все не просто, а очень просто с программной точки зрения.
Исходное уравнение:

А дальше я заменю производные на их определения:
https://akostina76.ucoz.ru/blog/2020-09-07-6728
Первая производная это приращёние функции, делённое на приращение аргумента функции. В данном случае функция от двух аргументов (x и t). Но записать как первую так и вторую производную конкретного аргумента можно и довольно просто.
Вот так, например:
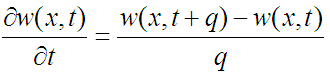
Или так:
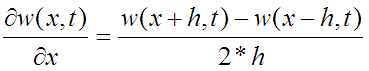
Запись производной по x немного отличается от общепринятой. Но и так можно записать. В теории есть бесконечно малый промежуток h. В компьютере он станет просто малым приращением. 2*h – это либо два бесконечно малых, либо два просто малых значения, что всё равно мало. Короче, так тоже можно записать определение производной.
Вторую производную по x можно получить из первой (проделав с ней то же, что было сделано с исходной функцией для получения первой производной). Будет так:

А дальше эти определения производных примитивно подставляются в исходное уравнение, исходя из того, что на малых промежутках отличая от реальных значений – величины какого-то N+1-го порядка малости:
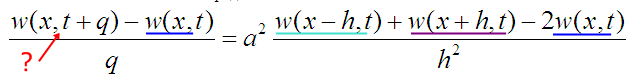
Единственное, чего я в этом не знаю это w(x,t+q), т.е значение температуры в следующий момент времени в некоторой точке x. Все остальное, что есть в уравнение, это данные по температуре в предыдущий момент времени. Они все мне известны. Это либо значения температур в начальный момент времени w(x,0):

….
либо полученное расчётом раньше (предыдущий ряд),
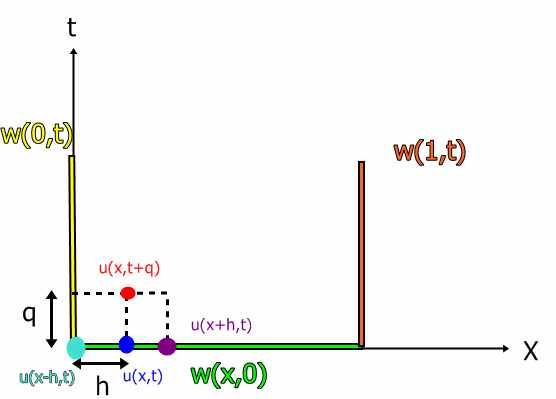
Довольно важно то, что надо знать всё, что на краях. Не только то, что есть в начальный момент времени по всей стенке ни и температуры на краях во все моменты времени. Без этого просто не посчитать значения u(x, t+q) на всех рядах кроме первого.
Потому количество известной информации будет на каждом шаге сокращаться. В погодной задаче будет именно так. На каждом следующем шаге будет отваливаться граничные точки. Ведь чтобы посчитать значения в них надо знать что там, откуда ветер. А эта информация есть только в начальный момент. Поэтому размер территории должен быть достаточно большой, чтобы смоделировать все перемещения воздуха, который в итоге через неделю попадёт в интересующую точку.
Весь текст расчёта для уравнения теплопроводности:
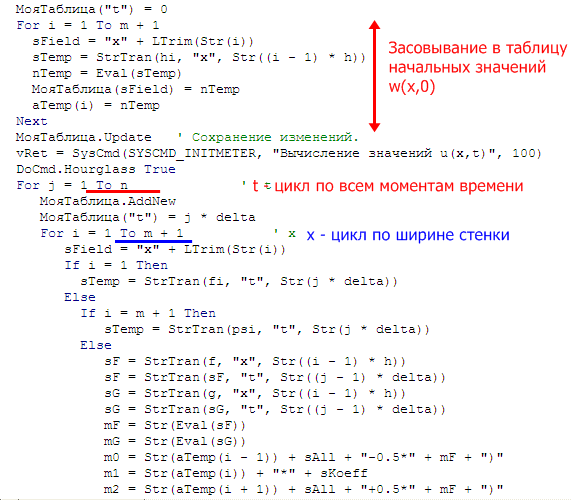
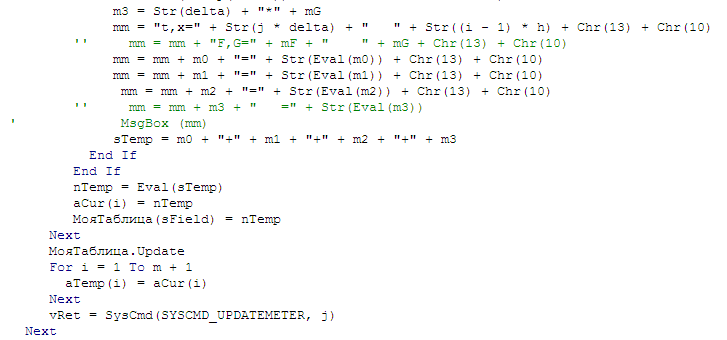
Вот и всё. И даже в этом половина строк – компиляция произвольных функций.
К уравнению теплопроводности можно что угодно и где угодно прикрутить. Моё задание было такое:
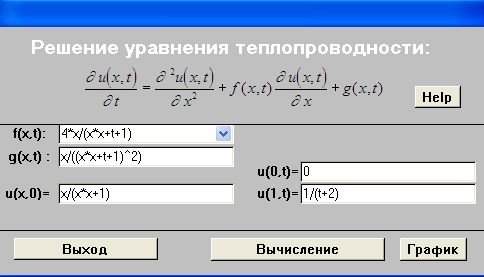
Расчёт почти не меняется. Ещё там чего-то присуммировать. И даже не обязательно брать уравнение теплопроводности. Можно взять вообще любое дифференциальное уравнение, заменить в нем производные на их определения и получить результат.
Единственное, что и на этом этапе (численный расчёт) может возникнуть совершенно неожиданная подлянка. Для этого уравнения (для остальных не помню), при расчёте надо соблюдать такое условие на шаги-приращения:

Если это условие не соблюдается, то получается не помню что, но очень высокохудожественное. Предмет «Методы вычисления» дополняет и так известные определения производных этой необходимой при машинном расчете информацией. На самом деле, довольно неожиданно что всё это работает только при определённых условиях.
Это я про то, что «машина посчитала» не всегда аргумент. Машина много чего посчитать может, и выдать очевидную лажу когда вроде бы, всё правильно написано.
|









