Довольно простой и уже неоднократно помянутый пример пластинки на двух пружинках, которую обдувает поток ветра V:
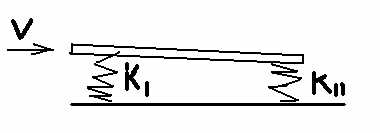
На самом деле это вовсе не пластинка на пружинках, а крыло самолёта, прицепленное креплениями в фюзеляжу. Жесткости пружин k1 и k2 – это жёсткости-прочности креплений крыла спереди и сзади.
Сразу оговорюсь: формулы, которые я нарисую ниже могут быть более неряшливыми чем надо. Дело в том, что итоговый результат, который я хочу показать я помню, но, естественно, не помню, как он выводился. Найденный пример похожей задачи… то ли тоже неряшлив, то ли я уже чего-то не понимаю. Так или иначе полностью правильное (если неточно это) будет отличаться от того, что ниже только расстановкой констант, а не выводом о поведении системы.
Выглядит это всё примерно так:
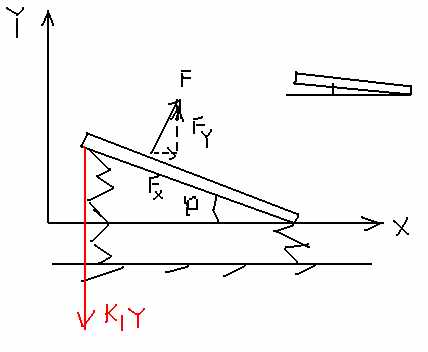
На пластинку действует подъемная сила F и сопротивляющиеся ей силы креплений, k1*y, где y – растяжение «пружины» (+k2*y).
Реально угол вовсе не такой большой, как на основной картинке. Реально он мал и всё выглядит как на картине в правом верхнем углу. А это означает, что я могу пренебречь лобовым сопротивлением Fx, т.е считать, что оно равно нулю.
y (т.е растяжение пружины) = L (длина пластинки) * sin(φ). Но из-за всё того же малого угла φ я могу заменить sin(φ) на φ. По известном из математического анализа примерному сходству этих функций вблизи нуля: lim(sin(x)/x) = 1 при x=0. Подробно про это тут:
http://akostina76.ucoz.ru/blog/2015-11-17-2193
(17.11.2015 Математический анализ)
… т.е из-за малых углов я фактически заменяю наклон на его отсутствие:

И в этом упрощённом варианте на конец пластины действуют две противоположно направленные силы – подъемная сила и реакция пружины, точнее пружин.
Если всё это вообще способно как-то лететь, сохраняя прочность и целостность, то это означает, что действующие в системе силы как-то, но уравновешены. Это означает, что поднялась пластинка под воздействием силы ветра на какую-то величину и будет оставаться в таком положении пока на неё действует постоянная подъемная сила F, вызванная потоком ветра V.
Но интересно, что будет происходить с системой если по каким-то причинам возникнет отклонение от этого равновесия (порыв ветра откуда-нибудь прилетит или ещё что-то). Такие вещи должны вызвать дополнительное малое отклонение системы от положения равновесия, т.е было отклонение пластинки от горизонтали на угол φ. Теперь к нему добавится какое-то малое отклонение dφ, которое и будет меняться во времени по какому-то закону.
Оно (это дополнительное отклонение) и будет тем самыми колебаниями вокруг положения равновесия (или же вместо колебаний начнётся разрушение).
Какой-то из основных законов пишется так:
F = m * a,
т.е ускорение объекта, помноженное на массу равно силе, которая это всё вызвала. Ускорение – это вторая производная от перемещения, т.е x’’. У меня на картинке не «x» а «y», но он же ещё почти равен углу φ, из-за всё той же малости углов. Потому я могу записать тот же закон так:
F = Q * φ’’ (или что одно и то же так: F = Q * (dφ) ^2)
Q – какая-то константа конструкции (поскольку константа, то сейчас не важно что это). Понятно, что у меня тут не масса, а что-то другое, но это не важно. Важно, что F ( итоговая) это всё та же разность подъёмной силы и реакций опор, потому:
Q * φ’’ = Fп - K dφ
Подъёмная сила (закон/теорема Жуковского?) Fп = Сy * ρ*V^2 * dφ /2.
Подставив получится так:
Q * φ’’ + (K - Сy * ρ*V^2 /2 ) dφ = 0
Вольно меняю знаки дифференциалов – производных на однотипные:
Q * φ’’ + (K - Сy * ρ*V^2 /2 ) φ’ = 0
Убираю Q, т.к оно портит мне внешний вид уравнения (на самом деле это означает, что я всё на него делю, и всё кроме φ’’ приобретает дополнительный коэффициент. Подъёмную силу тоже для краткости заменяю а константу Ry = Сy * ρ*V^2 /2.
Получится так:
φ’’ + (K - Ry ) φ’ = 0
или даже так:
φ’’ + A *φ’ = 0
Важно то, что решение уравнения принципиально отличается при разных знаках A. Если A>0, то будут затухающие колебания, если A<0, то амплитуда будет расти и будет разрушение.
Решение дифференциального уравнения:
http://matematikam.ru/calculate-online/differential-equations.php
|
A>0:
|
A<0
|
|

Уменьшение
|

Рост
|
|
Подставляю для проверки:
Exp(-x)’ = - exp(-x)
Exp(-x)’’ = exp(-x)
exp(-x) + (- exp(-x) ) = 0
|
Подставляю для проверки:
Exp(x)’ = exp(x)
Exp(x)’’ = exp(x)
exp(x) - exp(x) = 0
|
Рисование графиков:
http://matematikam.ru/calculate-online/grafik.php
На графике это так:

В данном уравнении хотя бы результатом является одна и та же функция – экспонента (exp), хотя и ведёт на себя совсем по разному.
А в таком дифференциальном уравнении: y’’+Ay = 0 изменение знака всего лишь константы приводит к тому, что система начинает вести себя принципиально другим образом, т.е двигается по другому «закону»:
|
A>0
|
A<0
|
|

|

|
|
Проверка:
Sin(x)’ = cos(x)
Sin(x)’’ = -sin(x)
-sin(x) + sin(x) = 0
|
Проверка:
Exp(x)’ = exp(x)
Exp(x)’’ = exp(x)
Exp(x) – exp(x) = 0
|
На графике так:
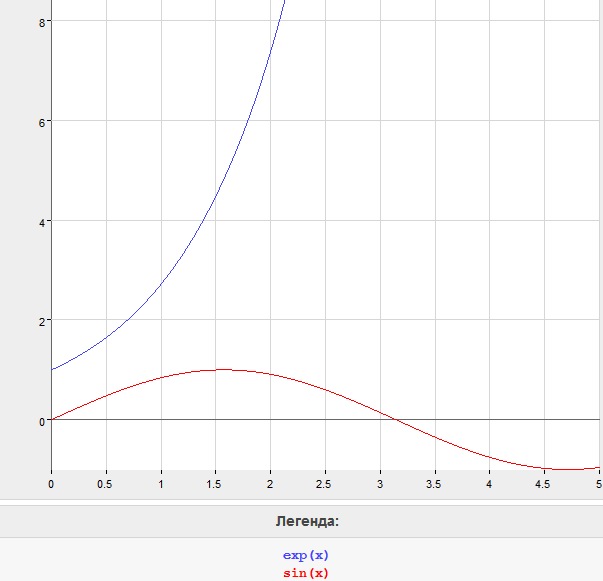
Уравнение, задающее «закон» одно и то же, но сложно придумать что-то что лучше бы иллюстрировало принципиально отличающееся поведение системы.
Возвращаюсь к пластинке на пружинах
φ’’ + (K - Ry ) φ’ = 0
или так:
φ’’ + A *φ’ = 0
A = K – Ry должно быть > 0
«К» это нечто, в которое засунута зависимость угла наклона φ от двух жесткостей пружин k1 и k2.
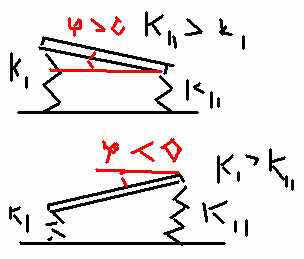
Грубо говоря, K = k2-k1. Тогда получается, что если k1>k2, т.е K<0, то A, который определяет поведение будет меньше нуля при любых значениях скорости набегающего потока, т.е точно сломается при любой скорости. Если же k2>k1, т.е K>0, то всё нормально. Будет летать, если конечно значения скоростей ветра не будут подходить к критическому значению для данной конструкции (что, опять же сделает A =k2-k1-Ry отрицательным).
Не все дифференциальные уравнения, тем более их системы решаются просто. Некоторые вообще решаются только численно. А с некоторыми можно как-то исхитриться. В примере модели «хищник-жертва»:
http://akostina76.ucoz.ru/publ/4-1-0-33
… например, написано так вместо функций, являющихся решением:


… кто такой «первый интеграл» я не помню, но возможно получить значения отдельных функций нельзя, а выцарапать что-то в виде перевязанных значений, годных для изображения на такой плоскости можно. Это и сделано.
| 








