Формула Фурье для волнового уравнения и простейший пример

Всё-таки надо аккуратно вывести до конца, то, что почти доделано тут:
http://akostina76.ucoz.ru/blog/2017-03-01-3908

… хотя бы потому что в формуле очередная опечатка.
Итоговые выражения, полученные в прошлый раз:

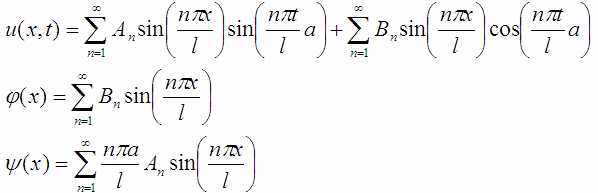
Общий вид разложения любой функции в ряд Фурье:

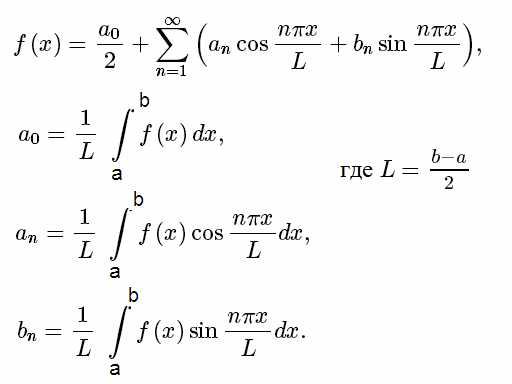
При этом ничто не мешает каким-то константам An и Bn быть нулевыми. Полученные формулы для начальных условий φ(x) и ψ(x) заставляют предположить, что эти функции раскладываются только по синусам, что означает, что все An из общей формулы разложения в ряд Фурье просто равны нулю. Это и то, что тут не произвольный отрезок [a,b] а отрезок [0,l] позволяет переписать общие формулы в упрощённом виде:

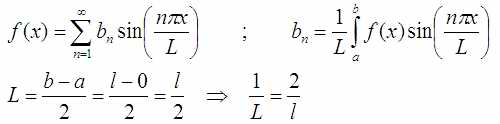
Довольно логичен вопрос как L заменяется на l в аргументе синуса. Ведь при замене должен возникнуть коэффициент «2». Видимо, это так получается:

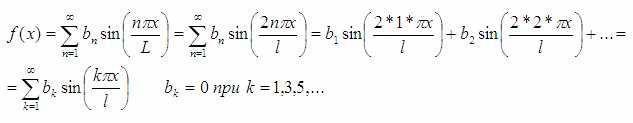
Просто обнуляются все нечётные коэффициенты так и так бесконечной суммы.  Предполагается, что функция и её искомые коэффициенты ведут себя описанным выше образом (полученном при выводе формул для φ и ψ)
Если собрать всё вместе:
 
Замена переменной в интеграле (x на y) просто чтобы заменить на что-то «x» в формуле для любой функции f(). Там может быть любая буква, т.к интеграл определенный и после вычисления его внутренняя переминая всё равно исчезнет, а значение будет какой-то цифрой.
Такое вольное отбрасывание кучи констант из общей формулы производит несколько неприятное ощущение неочевидности. Что-то строго доказывать, а тем более думать мне лень. Но неплохо бы хотя бы проверить на простом примере работает эта формула вообще  или нет.
Простых примеров у меня скопилось уже довольно много, но пусть это будет самый простой пример:
http://akostina76.ucoz.ru/blog/2017-02-17-3863

a=2, φ(x) = sin(x*π/5), ψ(x)=0, на участке x=0..5.
Коллекция коэффициентов An зависит от ψ, которая равна нулю. Значит они все нулевые, а общее решение имеет вид:

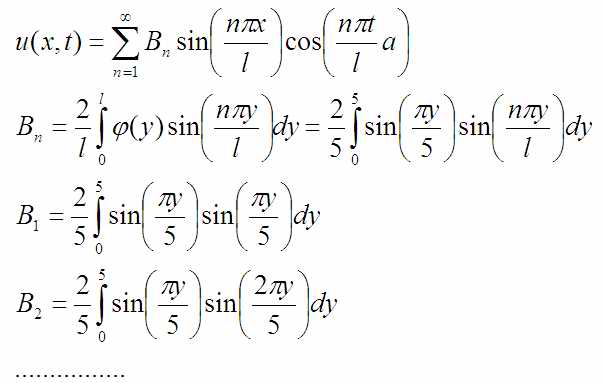
В порядке развлечения посчитаю эти интегралы без Maple. Чтобы взять интеграл от произведения синусов из него надо сделать сумму синусов/косинусов или других простых для интегрирования функций. Это делается по известным формулам преобразования тригонометрических функций:
 
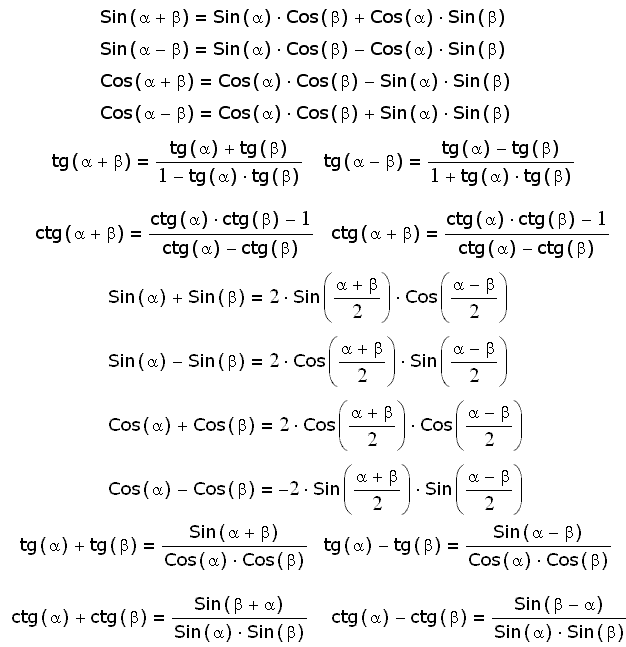
Поскольку мне встретилось произведение синусов меня интересуют третья и четвёртая строка. Из четвёртой я вычту третью и получу такое:

Чтобы не проверить это хотя бы Mapl-ом надо дойти до полного очумельства, потому проверяю:

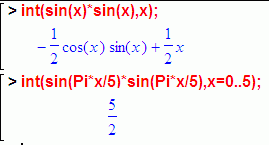
Совпало. Только Maple ещё зачем-то разложил синус двойного угла по первой формуле отсюда:

Итого первый коэффициент:

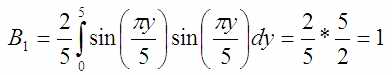
Уф…
Второй коэффициент:

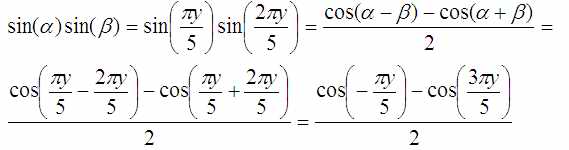
Почётную задачу интегрирования всего этого и аккуратного вытаскивания коэффициентов можно поставить Maple, хотя уже видно, что тут всё обнулится:
f:=(y)->(cos(-Pi*y/5)-cos(3*Pi*y/5))/2;
int(f(y),y);
int(f(y),y=0..5);

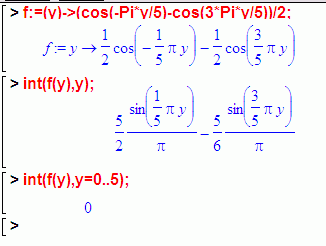
При вычислении интеграла подставлять  в синусы придётся либо y=0, а синус нуля равен нулю, либо y=5, но это проводит к выражению sin(π*k), которое тоже всегда равно нулю:

Точно также обнуляться все последующие Bn.
Итого решение для этого случая начальных условий принимает вид:

Но у меня уже было получено решение для того же уравнения с тем же начальным условием.
http://akostina76.ucoz.ru/blog/2017-02-17-3863

Оно выглядело так:

Можно для начала проверить равенство чисто визуально, т.е засунуть во всё тот же Maple и сравнить внешний вид:
u(x,t):=(sin( (x-2*t)*Pi/5)+sin( (x+2*t) *Pi/5))/2;
g(x,t):=sin(Pi*x/5)*cos(Pi*t*2/5);
plot3d({u(x,t),3+g(x,t)},x=0..5,t=0..10,axes=boxed);

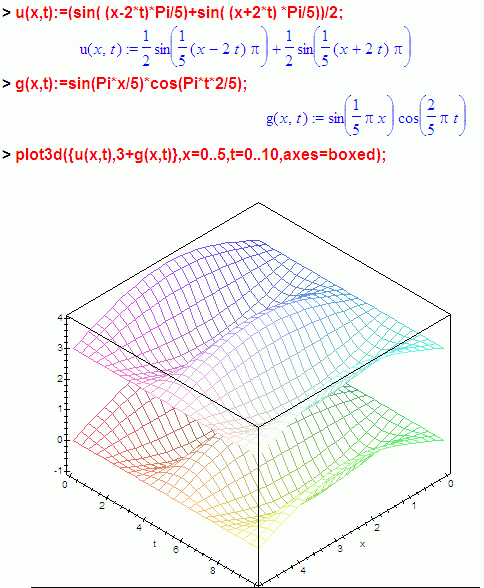
… Похоже, во всяком случае.
А раз похоже, то почти наверняка одно выражение можно перевести в другое с помощью всё тех же тригонометрических преобразований. Попробую. В данном случае мне потребуются первые две строки из списка тригонометрических преобразований:

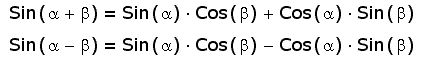
Ведь первое выражение это синусы суммы и разности. Вот его-то я и попробую раскрыть:

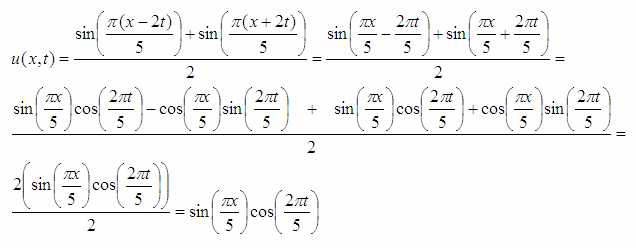
Для данного конкретного случая получилось доказать, что оба решения дают одинаковый результат. Решать задачу можно как угодно, но ответы должны быть одинаковыми. Если получились разные то неправильный либо один либо оба.
Кроме того выкладки выше – хорошая иллюстрация того как много тут мест, где можно ошибиться в элементарной арифметике. Потому существуют разнообразные проверки промежуточных выкладок хотя бы так как здесь показано: подставить в простой пример и проверить не закралась ли уже в вычисления какая-то шибка.
Похоже на анекдот, но рассказывали как настоящий эпизод. Кто-то рассчитывал дамбу, посчитал все нагрузки, получил какой-то результат. Во время защиты кандидатской кто-то на коленке подставил полученное решение в легко получаемые значения перемещений и получил, что эта дамба отдрейфует на 100 метров вниз по течению. Всякое бывает. Лучше проверять.