Композитные материалы

Среда, с которой привычно работает механика это так называемая гомогенная или однородная среда. Привычно работает это значит под такую среду давно разработан инструментарий с помощью которого можно рассчитывать то, как будет вести себя этот кусок железа при нагрузке или этот объем воздуха при обтекании крыла самолёта.
Понятно что не бывает железа без примесей и с аккуратной и одинаковой кристаллической решёткой. И в воздухе чего только не летает.
Гомогенная среда это придуманная упрощённая модель реальности, которая позволяет получать при обсчёте результаты, сходные с тем, что демонстрируют реальные среды. «Несовершенствами» реальных сред пренебрегают, и считают, что в каждой точке этой гомогенной среды свойства точно такие же как в любой другой точке.
При этом эти свойства вовсе не обязаны быть одинаковыми по всем трём измерениям. Например можно учесть что у куска дерева прочность на разрыв вдоль волокон большая а поперёк волокон маленькая. Но это свойство таково во всех точках изучаемой деревяшки.
Гомогенные среды относительно просты. Это означает, что решение поставленной задачи можно получить аналитическими методами примерно также как можно получить X из уравнения 2*X = 3 выполнив несложные вычисления. Хоть сколько-нибудь реальные задачи аналитического решения обычно не имеют. Шестигранной гайки вполне достаточно чтобы никакая математическая изворотливость не смогла дать решение задачи.
Для решения таких задач используются численные методы, про один из которых было тут:
http://akostina76.ucoz.ru/blog/2016-11-16-3625

Т.е нечто любой формы как бы разрезается на очень мелкие кусочки. Кусочки считаются достаточно мелкими для того чтобы любую функцию на малом интервале можно было заменить её линейным приближением. Численный метод должен сходиться, т.е неизбежные погрешности вычислений должны быть небольшими и метод должен дать близкий к реальности результат. И кусочки должны быть мелкими и ещё какие-то условия для этого могут потребоваться. В уравнении теплопроводности, например, потребовалось чтобы delta/(h*h) было меньше 0.5.
Обычный численный метод при решении таких задач – так называемый Метод Конечных Элементов. Ничего кроме названия не помню, но название правильное.
Вот, например, видео с описанием программы обсчёта той самой любой конструкции (конструкции любой формы), в котором подробно показано как идёт процесс разбивки на мелкие элементы
https://www.youtube.com/watch?v=pjqvuDnH7V4&index=5&list=PLM66dyir0u2ctKIPmSloSdk-OSklESwMF

Процесс сам по себе не простой, но позволяет получить примерно такое для конструкции любой формы:

Дальше можно это всё считать, т.е то как будут деформироваться конструкции при нагрузках. Вот, например, лопасти вертолёта при порывах ветра оттуда же:
https://www.youtube.com/watch?v=y1zuxhm5Z-w&list=PLM66dyir0u2ctKIPmSloSdk-OSklESwMF&index=15

Т.е уже гомогенные среды поставили задачи, которые решаются только численно и для них уже придуман инструмент, позволяющий их решать.
Композитный материал это материал, состоящий из нескольких разных материалов. Причём это не сплав, а именно как-то соединённые отдельные куски с четкими границами между ними (на границах меняются свойства среды). Делается это например для того чтобы получить итоговый материал с характеристиками, которых нет у исходных материалов. Например бетон прочен при сжатии и имеет массу других полезных свойств. Но вот прочности на разрыв он почти лишён, а давления грунтов на фундамент например могут быть очень большими.
Стандартное решение – армирование бетона железными прутьями:

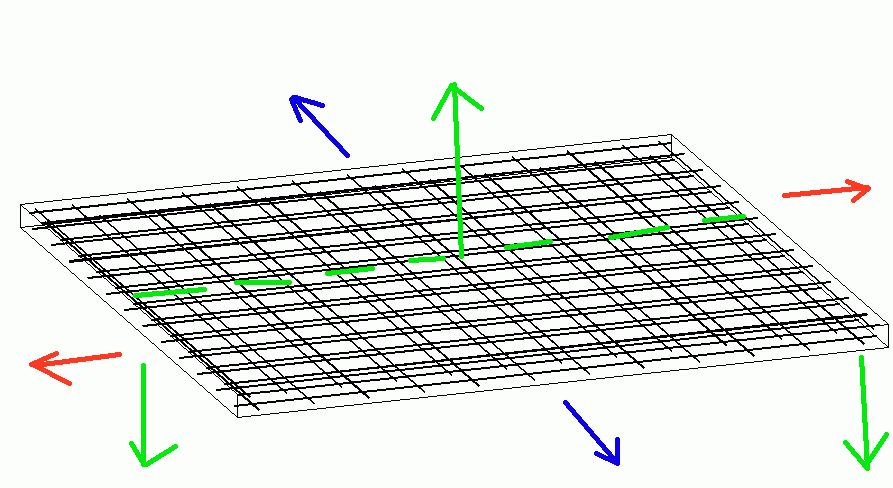
Такая конструкция уже и разрыв в двух направлениях (красное и синее) сдерживает и изгибаться (зелёное) не позволяет.
Второе популярное использование – фанера. Естественные волокна дерева очень прочны в одном направлении. Но тонкий лист почти лишён прочности поперёк волокон. Но если склеить несколько листов под разными углами, то прочность дерева по всем направлениям будет одинаковой.
Армирующие волокна – не единственный вариант композита. Абразивный круг, например, это зерна твердого режущего материала, залитые связующим «клеем» (связкой).
Мельчайший кусок абразивного круга выглядит примерно так:

Причём это именно та модель, которая используется при обсчёте характеристик материала хотя зерна, конечно, не обязаны лежать так ровно. Но у этих кругов кроме твёрдости:
http://delta-grup.ru/bibliot/39/10.htm

… есть ещё какой-то связанный с ней параметр, который не может быть больше 0.5. А это максимальное соотношение объемов шара и куба, в который он вписан.
При вот таком максимальном варианте:

… когда шары напиханы так, что больше уже не засунуть это соотношение 0.52.
Обычно то, что придаёт прочность (железные прутья в бетоне и режущие зёрна в абразиве) в композитах называются ВКЛЮЧЕНИЯМИ. А связующий материал (бетон или связка) МАТРИЦЕЙ.
И включения и матрицы могут быть сделаны из любого материала. Например автомобильный пластик сложной формы это обычно всё те же придающие прочность на разрыв «тряпки» залитые какой-то мастикой.
Рассказывали, что корпуса самолётов из композитов делают. Корпус самолёта с механической точки зрения это тонкая оболочка. А тонкое всегда потенциально непрочное. А перевязанные нити включений композита позволяют обеспечить нужную прочность и одновременно дать малый вес свойственный пластикам. В авиации это особо важно, т.к чем легче самолёт тем меньше он есть горючего. Отсюда, в свое время и началось повсеместное использование лёгкого металла алюминия вместо привычной стали.
Обсчёт композитов конечно тоже только численный. Но все методы уже разработаны. Просто при расчёте надо учитывать, что с некой границы часть мелких кубиков имеет какие-то другие параметры. Даже метод, подозреваю, менять не надо. Обычно параметры материала это одна общая для всего расчета константа. А тут будет например два значения, которые будут чередоваться от слоя к слою (от точки к точке).