Напряжения, деформации, прочность (метод конечных элементов)
Здесь:
https://akostina76.ucoz.ru/blog/2020-09-24-6767
… у меня был заданы начальные температуры в стенке ( w(x,0) ). Это называется «начальные условия». А ещё мне пришлось задать изменения температуры с двух сторон стенки ( w(0,t) и w(1,t) ). Это называется «граничные условия». Без всего этого мне бы не удалось выполнить этот численный расчёт.
В случае уравнения теплопроводности обычно интересно знать, что будет через некоторое время с уже нагретым (как-то) предметом. И обычно же непонятно, откуда брать эти условия на границах. Они довольно часто и интересуют (а не то, что там внутри).
А в случае исследования прочности граничные условия, как правило, известны. Они и вызывают всё происходящее. Стоит кран, к нему (по классике мультипликации) подведен груз. Вес груза (т.е напряжение на границе) известен. Узнать надо, как продеформируется кран и какие в нём будут напряжения (не выйдут ли они за предел прочности).
Напряжение на границах, конечно, могут меняться. Только известно, как они меняются. И по ним можно вычислить то, что происходит в исследуемой детали.
Результат расчёта решения уравнения теплопроводности в меня был получен в виде такой таблицы:

Всю метровую толщину стенки я разбила на 5. Потому в итоговой таблице появились температуры в точках x=0.2, 0.4 и т.д. Мне показалось, что мне этого хватит. Можно увеличить точность расчёта, разбив метр на 100 или даже больше.
Шаг по времени я взяла такой, чтобы не нарушалось условие сходимости. Что тут назвать «расчётным узлом» - вопрос вкуса. Можно скачать, что узловые точки в этом расчёте – точки по x. А можно назвать расчётными узлами комбинацию координаты x и времени t. При численной решении всегда есть такие узлы, образующие расчётную сетку.
Очень приятный плюс численного решения в данном случае возможность задать параметры не константой, а функцией. Какая мне разница, какое значение подставлять в расчёт в конкретной точке в конкретный момент? Могу константу. Могу значение функции. Эта возможность означает, что я запросто могу считать и для композитных материалов. В каких-то точках будут одни параметры (плотность и т.д),а в других другие. Параметры материалов могут меняться со временем (из-за изменения температуры, например). И эти особенности поведениям материалов, которые обычно мгновенно делают задачу принципиально другой (и принципиально иначе решаемой) численный расчёт почти «не заметит». Небольшое усложнение в тексе, не более того.
При расчёте напряжений и деформаций в методе конечных элементов:
http://ntp-dip.ru/study/
… всю трёхмерную штуковину делят на «кубики»:
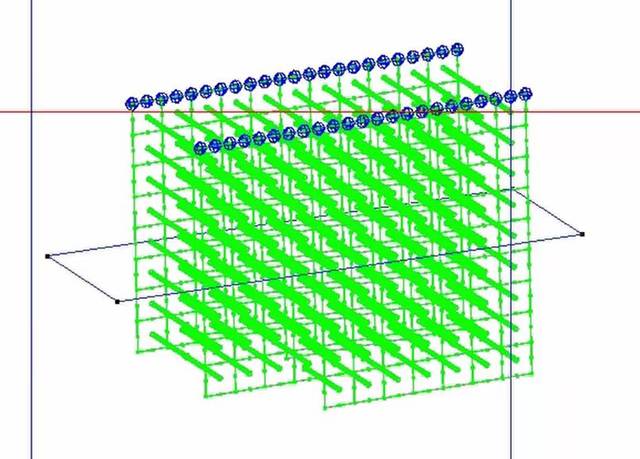
Эти кубики не всегда совсем кубические:
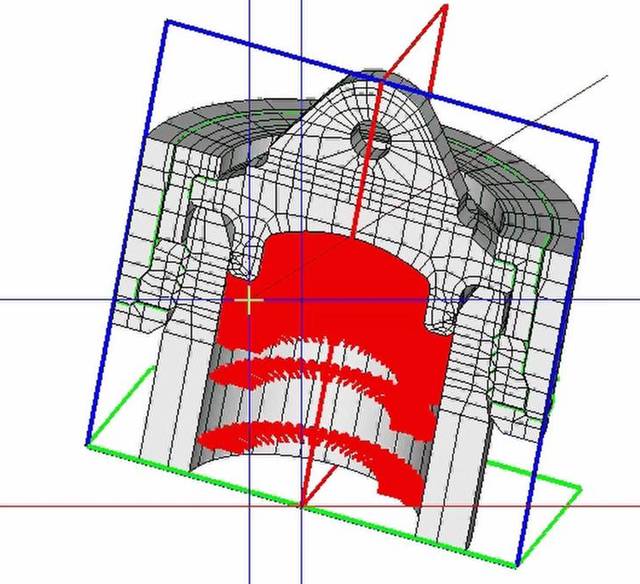
… потому что форма может быть такой, что кубики неудобно. Но всё равно перед расчётом придумываются расчётные узлы, по которым (и в которых) всё и будет считаться. Насколько поняла, в Zenit-95, эти узлы можно и изменить. Не факт, что машина выберет лучший вариант разбивки.
Как бы то ни было, есть какая-то разбивка на те самые конечные элементы. А дальше считается всё, что интересует (обычно напряжения и деформации) в ближайшем к приложению нагрузки кубике. После этого волна расчёта идёт дальше. Для ближайшего к нагрузке кубика все известно. Значит известно и как он влияет на следующий кубик. Уже его воздействие становится граничным условием для следующего кубика и всё повторяется.
Можно повысить точность, увеличив количество узлов. Программа при этом не измениться, увеличится длина циклов и, потому, время расчёта. Допускаю, что можно попытаться взять не определение производной (см. текст по ссылке) а разложение функции в ряд Тейлора. Тогда отбрасываемое (по идее) будет ещё мельче (следующего порядка малости). Но всё равно, как и в случае теплопроводности, расчёт в программе, в которой заложен алгоритм «Метод конечны элементов» будет не сложным и не длинным. Не длинным с масштабах программных текстов. Длинный программный текст будет для какой-нибудь бухгалтерии, в которой куча справочников и документов. И для всего этого нужны почти отдельные но, всё-таки, отдельные тесты. Одни и те же алгоритмы будут повторяться десятки раз, но они все будут в программе.
Здесь же один алгоритм. Он сложнее расчёта финансового отчёта, но он все равно один.
Потому меня и озадачили 7 Gb программы с этим самым Методом Конечных Элементов. В Zenit-е в этом 90 % кода, скорее всего, обработка прорисовки и вращения штуковины на экране, а не сам расчёт. Муторно, но и это при желании можно сделать. Это и сделали. Чего-то оно тоже занимает. Из-за этого их архив 94 Mb. Примерно так и должно быть. Какой расчёт чего может занимать 7 Gb места?
|









