Немного про графики

Чтобы увидеть, как бегут волны при решении волнового уравнения надо задать два начальных условия: начальную форму и начальную скорость.
По этому поводу напомню основные операции с графиками.
Если я хочу чтобы у меня волна бежала, то, наверное, вначале должно быть по форме что-то напоминающее волну. Очень хорошо для этого подходит вот такая функция:
f(x):=1/exp(x*x);

Что-то маловатый какой-то график получился. Хочу увеличь высоту «горба» и потому умножу его, например, на 3:
f(x):=3*1/exp(x*x);

А теперь я, например, хочу чтобы «горб» стал поуже. Я умножаю аргумент экспоненты (exp) на 10:
f(x):=3*1/exp(10*x*x);

Если я наоборот захочу его растянуть вдоль оси X мне надо будет умножить ни на 10 на 0.1.
Пусть у меня есть синус:
f(x):=sin(x);

А я, например, хочу чтобы первый «горб» был не от 0 до Пи, а от 0 до 5.
Это означает, что аргумент синуса должен сдвинуться по такому правилу:
sin(Пи)->sin(5*x). Это означает, что коэффициент = Пи/5.
Итоговый вариант:
f(x):=sin(x*Pi/5);

Пи/5 меньше 1 (примерно 3/5=6/10=0.6)
Так выглядят три синуса, сжатые или растянутые разными коэффициентами:
plot([sin(0.5*x),sin(x),sin(1.5*x)],x=0..2*Pi,color=[red,blue,green]);

… т.е если коэффициент меньше 1, то график растягивается вдоль X, если больше 1 то сжимается.
Пусть я хочу изобразить нечто, похожее на ступеньку, на интересующем меня интервале от 0 до 5. Тогда мне надо растянуть синус по оси X как это было сделано выше, сжать его амплитуду и приподнять график над осью X. Сжимать я буду до высоты «горба» равной 0.2, а поднимать на 2. Будет так: 2+0.2*sin(Pi/5*x)

Если я хочу чтобы «ступенька» была отрицательной, мне достаточно поставить знак минус перед функцией:
plot([2+0.2*sin(Pi/5*x),-(2+0.2*sin(Pi/5*x))],x=0..5,color=[red,blue]);

Теперь про интегралы. У меня были сомнения, определение это было или теорема, но вроде теорема:
https://www.math10.com/ru/vysshaya-matematika/integrirovanie-diferencirovanie.html

Если по-простому, что интеграл – это площадь под графиком от какого-то X1 до какого-то X2:

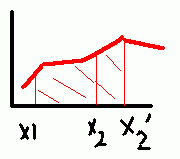
Но ведь двигая эти интервалы будут получаться разные значения площади под графиком. А разнее цифры, привязанные к разным точкам X тоже вполне логично рисовать в виде графика.
Здесь:
http://akostina76.ucoz.ru/blog/2017-02-08-3835

… у меня производная превращала прямую линию под углом в строго горизонтальную линию, а параболу в наклонную линию.
Можно посмотреть, как это действует в обратном направлении.
 

Считать надо площадь под прямой линий и рисовать зависимость этой площади от X. В случае прямой линии считать совсем просто. Достаточно посчитать сколько квадратов со стороной = 1 уже попало в площадь. Понятно, что в точке 1 это 2 «круга», т.е значение функции заданной интегралом этой горизонтальной прямой =2. А в точке 2 это 4. И т. д. Видно, что функция, полученная вычислением площади полностью повторяет начальный вариант функции.
Тоже самое для параболы:
Y=X*X/2:

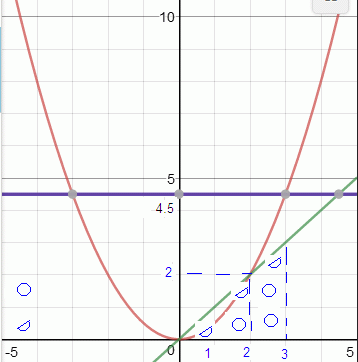
При X=2 площадь под прямой это один целый квадрат и две половины, т.е 2. При X=3 площадь это 3 целых квадрата и три половины. Это и есть 4.5 при том, что Y(3)=X*X/2=3*3/2=9/2=4.5.
Определённый интеграл обозначается так:

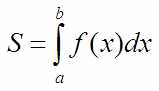
Это не функция, а константа, конкретная площадь. Ведь тут всё задано и сама функция и конкретный интервал (от a до b).
Пусть существует некая функция g(x), такая что, её первая производная равна f(x). Тогда можно написать так:

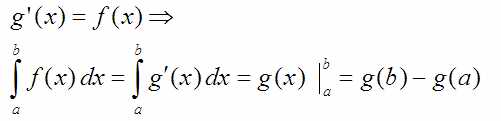
Это просто правило вычисления интеграла, означающее что площадь под графиком от точки a до точки b равно всей площади под графиком от минус бесконечности до b минус площадь от минус бесконечность до a:

А раз так, то можно задать и некую функцию от x через интеграл от другой функции и её значения определить,  например, так:

При этом функция G(x) вовсе не обязана быть отлична от нуля весть интервал до бесконечности. Она может быть например нулевой при x<0.
В самом начале текста у меня единственный «горб» выражался через экспоненту.  
Начальный и конечный вариант этой экспоненты выглядят так:
plot([1/exp(x*x),3/exp(10*x*x)],x=-5..5,color=[red,green]);

А так выглядят интегралы этих функций:
plot([int(1/exp(x*x),x),int(3/exp(10*x*x),x)],x=-5..5,color=[red,green]);

Видно, что более высокий и сжатый вариант по форме ближе к ступеньке.
А для совсем ступеньки существует дельта-функция Дирака, которая равна бесконечности в нуле и нулю, во всех остальных точках. При этом считается, что за этот бесконечно малый момент она набрала площадь равную единице. Интеграл от неё выглядит так:
plot(int(Dirac(x),x),x=-3..3);

Т.е пока всплеска не было интеграл равен нулю, а как только он был, то не важно насколько давно он был, всплеск площади уже до плюс бесконечности остаётся равным нулю.
С помощью дельта – функции Дирака моделируются ударные воздействия, когда до ничего не было и после ничего не было, но был очень короткий момент удара, изменивший движение.