Обсчёт колебательного LC- конутра

Мои электрические познания, не смотря на все недавние тексты, - развитие схемы фонарика из батарейки и лампочки. Постоянный ток мне понятен и привычен. А вот ток переменный – это то, что именно непривычно (для начала). Потому у меня есть желание «побродить» тут вокруг «маленькими шажками».
Сомневаться в формуле для резонансной частоты колебательного LC-контура довольно странно. Но вот попытаюсь я её вывести вручную. Так, для тренировки.
Колебательный контур это соединённые параллельно индуктивность (L) с конденсатором (С):

На картинке к ним прицеплен тот самый переменный ток. Утверждается, что при определённой его частоте возникает резонанс. Пока не важно, что это такое. Важно, что происходит нечто, чего не бывает при других частотах.
Конденсатор и индуктивность пропускают переменный ток. Как и полагается электрическим компонентам, в них при этом возникает какое-то сопротивление. Только в данном случае оно зависит от частоты тока. Обычно такие сопротивления называют реактивными.  А я их в расчётах буду помечать волной.
Известно, что сопротивления конденсатора и индуктивности считаются по формулам:

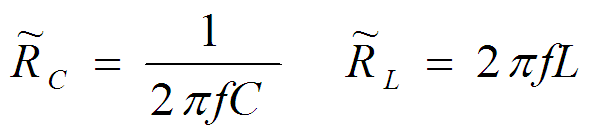
… где f – частота колебаний тока, C – ёмкость конденсатора, L – индуктивность катушки.
Раз проводники подключены параллельно, то можно посчитать сопротивление в этой цепи по стандартной формуле:

Просто всё подставляю:

У меня получилось не просто так формула, а выражение, показывающее общее сопротивление цепи (её зависимость от частоты), поведение которой я пытаюсь понять. Обычно его пытаются понять по виду полученной функции, по тому возрастает функция, убывает, есть ли у неё минимум и максимум. Довольно часто в таких экстремумах (минимумах и максимумах) происходит всё самое интересное.
Чтобы было проще и привычнее писать, а поменяю переменную:

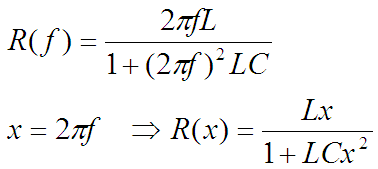
Довольно легко понять, как выглядит эта функция. До какого-то момента сильнее компонента L*x (при чем, в данном случае она сильнее прижимает график к нулю). Ведь x*x в знаменателе мала при малых x, а делитель =1 не важен. Но с ростом x знаменатель начинает расти и делит это Lx на всё большее значение. Короче, явно у этой функции есть какой-то максимум. Он там и есть. Итоговая функция зелёная:

И у неё действительно есть где-то максимум. Осталось узнать его координату.
Координата максимума (или минимума) – это точка, к которой равна нулю первая производная. Не чувствую в себе сил ни считать производную ни, тем более, приравнивать её к нулю. По стандартным и простым формулам это считается, но уж очень муторно.
Вот результат:

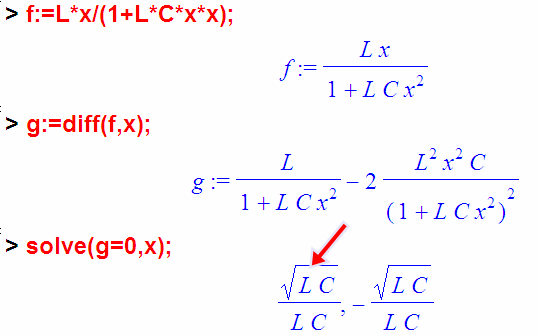
Отрицательное значение возможно с математической точки зрения, но не возможно с физической. Т.е ответ один (тот, на который стрелка указывает). Это и есть координата «горы». Остаётся вернуться обратно от x к частоте f:

 
Полученное – формула для резонансной частоты. А по всему расчёту выше видно, что это частота, при которой общее сопротивление цепи максимально (на графике, увы «гора» а не «яма»)
Максимальное сопротивление выглядит сомнительным счастьем. Ведь чем больше сопротивление, тем меньше ток. Но что есть, то и используется.
Большое сопротивление, например, может вытащить на себя большее напряжение при последовательном соединении. Если подключить так (т.е контур последовательно с R1):

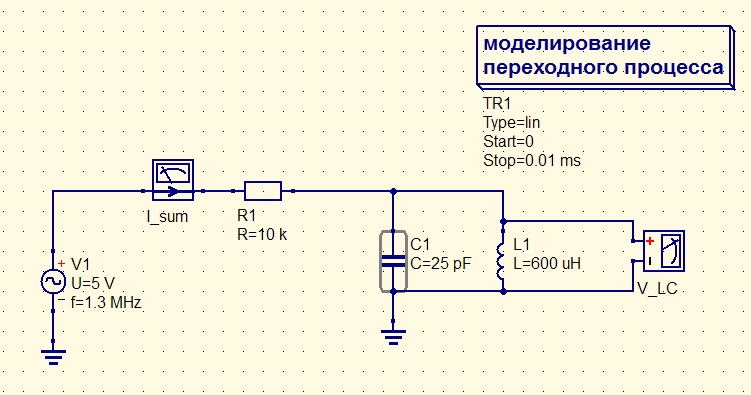
… то контур (на резонансной частоте) вытащит почти 5 вольт напряжения:

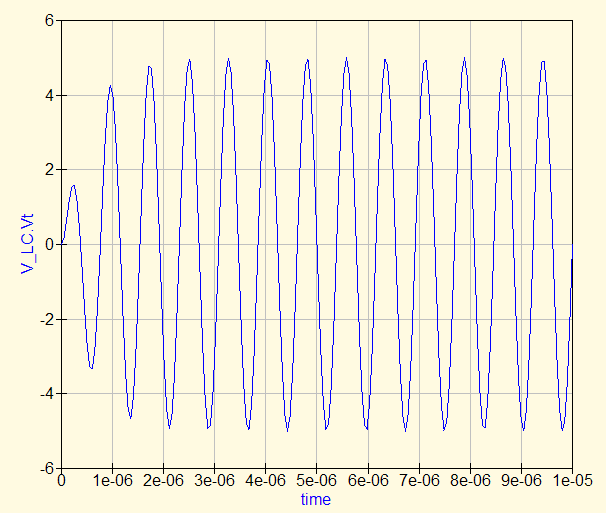
На частоте в 10 раз больше резонансной:

… сопротивление мало. Потому падения напряжения на этом участке почти нет:

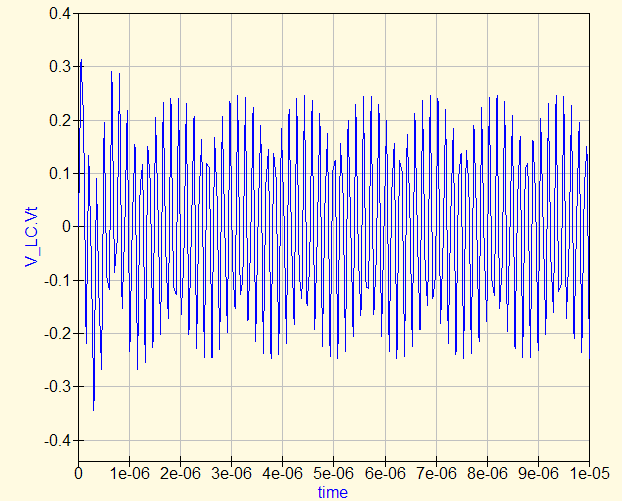
Всё достаётся резистору R1.