Основные буквенные обозначения в физике и математике

Не знаю уж насколько они основные. Всякое бывает. Начну с латинского алфавита.
 

(x,y,z) – обычное обозначение координат в трёхмерном пространстве.
a,b,c – обычное обозначение любых констант моделей.
При этом довольно часто для обозначения зависимости переменных недостаточно одной константы «a». Может потребоваться целая матрица из 9 значений. Тогда она уже будет обозначаться большой буквой  «A»:

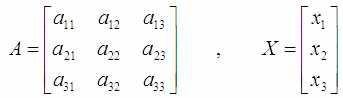
Но раз константа размножилась в матрицу с одинаковыми буквами но разными цифрами, то логично обычно неизвестную координату (x,y,z) обозначить точно также. Так появляется большая буква «X» - не параметр, в вектор из трёх неизвестных значений.
В винном расчёте:
http://akostina76.ucoz.ru/blog/2016-08-26-3357

… было использование этих матриц и векторов. Буквы становятся большими, но общий смысл сохраняется. X, Y, Z – обычно неизвестные вектора, A,B,C – известные вектора или матрицы.
Возникающая при решении дифференциальных уравнений константа обычно обозначается через «С», а если из там много, то C1, C2 и т.д.
«f», т.е f(x) – обычное обозначение функции. В паре к ней обычно идет g(x). Если этого мало или по каким-то причинам хочется использовать другой диапазон, то для тех же целей (обозначения некой функциональной зависимости) может использоваться компания u(x), v(x), w(x).
Довольно часто интеграл от «маленькой» буквы обозначается большой буквой:

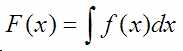
Счётчики в рядах (n,k,i,j):
http://akostina76.ucoz.ru/blog/2017-02-22-3882

Обычно используются в парах (n,k) и (i,j) например так:

Разные диапазоны позволяют примерно показывать о чём речь если приходится использовать сразу два объекта в которых зачем-то надо считать суммы.
Большая буква «N» - количество штук чего-то, например слагаемых ряда:
http://old.exponenta.ru/educat/systemat/savotchenko/7_4.asp

… если их не бесконечность.
Большая и маленькая буквы «0» зарезервированы исключительно для обозначения не учитываемых погрешностей (отброшенных слагаемых ряда). Используется только (!) для этого.
«d» может означать полный дифференциал, хотя в таком выражении её сложно с чем-то спутать:

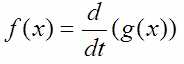
«t» довольно однозначно обозначает время.
«S» значительно чаще площадь, чем расстояние.
«h» - довольно частое обозначение шага в формуле для дифференцирования. Аналог Δx отсюда:
http://akostina76.ucoz.ru/blog/2017-02-09-3836

Если закончились свободные буквы для обозначения неизвестных функций то можно использовать пару p(x) и q(x) хотя это и нежелательно потому, что они уже довольно однозначно ассоциируются с физическим понятием давления и плотности некого свойства. Но и так используют, когда хочется что-то вынести в своеобразную отдельную группу.
Греческие буквы:
 

Написание многих букв такое же как в латинском. В таблице на таких прочерк, означающий, что не используется.
Довольно часто происходит переход в другую систему координат. Здесь, например:
http://akostina76.ucoz.ru/blog/2017-02-12-3846

… потребовалось сделать так:

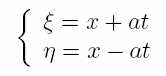
Алфавит позволяет сразу понимать в какой системе координат происходят операции. Если вдруг вместо привычных (x,y,z) что-то делается с (ζ, η, θ) то можно с достаточным основанием думать, что где-то выше в тексте был переход в другую систему координат.
Точно также обозначение функции греческими буквами φ(x), ψ(x) а не латинскими буквами другого диапазона или даже размера обычно призвано подчеркнуть, что это что-то принципиально другое, например известные начальные условия, а не искомая функция.
Как-то исторически сложилось, что углы обозначаются маленькими буквами α, β, γ. Видимо это пошло от древних греков с их треугольниками.
Зарезервированное и используемое только так:
1]  «Δ» Дельта (т.е отличие, разность), оператор Лапласа (точное значение из контекста)
2] «π» - число ПИ (3.14)
3] «Σ» - сумма
δ может означать вариацию (из вариационного анализа), но что-то очень маленькое она означает чаще. Например, здесь:
http://akostina76.ucoz.ru/blog/2016-02-15-2612

… зазор между зубцами ротора и статором.
«Ω». Точно не помню символическое заклинание. По-моему это было как-то так:

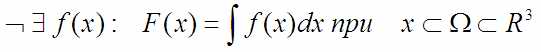
Здесь написано «Пусть существует функция f(x) такая что F(x) равно интегралу от f(x) при всех значениях х из некого множества координат Ω принадлежащего трёхмерному пространству»
Разные бывают пространства. Может быть например пространство только целых чисел, в которых не существует дробей.  А можно взять какую-то функцию и объявить пространством множество её значений. Перед тем как что-то писать, надо указать, с чем собираешься работать, в том числе и с каким пространством значений.
p/s
Просто для коллекции. Пока, вроде, не надо:
Знаки математической логики:
https://ru.wikipedia.org
grad (градиент), div (дивергенция), rot (ротор), оператор Лапласа:
grad, rot. div