Переменные Лагранжа и Эйлера
С движением воды и воздуха уже довольно давно всё примерно понятно. Но если у человека нет всего этого инструментария, изучая картинки типа погодных отсюда:
https://akostina76.ucoz.ru/blog/2020-07-30-6657
… он в какой-то момент будет вынужден попытаться ответить себе на вопрос «А что я хочу получить?»
Лагранж, скорее всего, наблюдал за деревяшкой, движущейся в какой-нибудь канаве со скоростью течения как я за тучей:
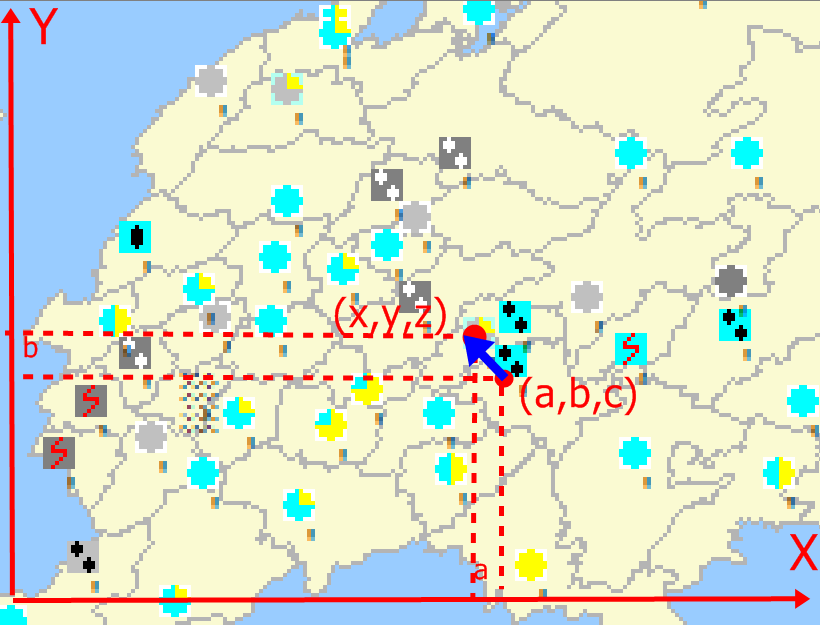
В начальный момент деревяшка– туча была в известной точке с координатами (в трёхмерном пространстве) – (a,b,c).
Решение задачи известно, если известно где она будет через некоторое время, куда будет двигаться, с какой скоростью. Ещё неплохо знать прочие параметры (температуру, давление, скорость).. Эти параметры будут значениями новой точки деревяшки – тучи (x,y,z).
Но эта новая координата – функция от начального положения, т.е:
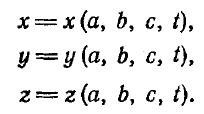
А значит все эти давления и температуры, который будут в точке с новыми координатами:
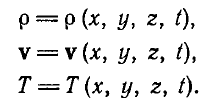
… на самом деле – функции от начальных координат. Для температуры так:
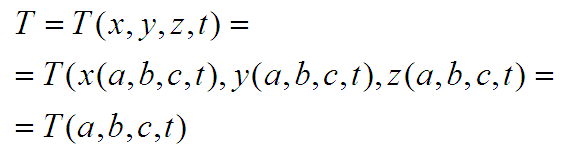
Для остальных – так же но другая буква.
Все вместе: решение задачи известно в переменных Лагранжа если известно вот это всё:

А Эйлер видимо исходил из того, что движение тучи – деревяшки это, конечно очень интересно. Но в случае погоды, например, я сижу в точке с конкретными координатами (x,y,z). А интересует меня, какая тут завтра будет температура и будет ли дождь.
Интересует состояние той малой, но не бесконечно малой частицы (из которых в этой модели все состоит), которая в данный момент оказалась в интересующей точке:

Наверное, Эйлер исследовал жидкости в трубах. И интересовало его давление в конкретной точке и вопрос, не порвётся ли там труба.
|









