Применимость моделей и численные методы

Вчера у меня получилось нечто странное с расчётом чайника:
http://akostina76.ucoz.ru/blog/2018-03-15-4903

… Моё сходу сделанное предположение, что в википедии напутали с размерностью… имеет право на существование но не обязано быть фактом.
Имеет смысл подробнее посмотреть на то, что делал Фурье в 1807 году, т.е на эксперимент, из которого он получил закон:
https://www.calc.ru/Zakon-Furye-Osnovnoy-Zakon-Teploprovodnosti.html
Не мог он тогда исследовать двухмиллиметровый пластик. Нечем было измерять температуру и время с доставочной точностью. А мог он исследовать стержень разной длины и диаметра нагреваемой с одной стороны разными по мощностями источниками тепла. Этим, скорее всего, и занимался. Получил (для своего эксперимента!)  такую зависимость:

Подчеркну, что нет тут никаких производных. Тут знак Δ означающий изменение величины. Знаком производной (любого вида) он может стать если сказать, что тут всё бесконечно малое. Но тут не так. Выбранный мной вчера промежуток времени в 30 секунд бесконечно малым никак не является. Эти значки означают именно такие промежутки.
Фурье, проводя свои эксперименты, всего лишь установил и записал, что чем больше разница температур тем больше отток тепла. И, наоборот, чем больше толщина стенки (=длина стержня в эксперименте) те меньше отток тепла.
А ещё у него получилось что величины связаны некой константой «k», т.е можно в разумных пределах менять геометрию исследуемого стержня и температуры, зависимость будет сохраняться через эту константу.
Изменение толщины стенки почти до нуля выходит за эти разумные пределы допустимой геометрии. Закон Фурье в этом случае даёт уход оттока на бесконечность потому что если что угодно поделить на ноль то та самая бесконечность и получится, а так не бывает. Чайник с тонкой стенкой возможно вскипятить – это доказательство того, что так не бывает.
В «Математической физике» Попова написано так:

Не поняла я, честно говоря, что тут написано но речь именно про границы применимости модели и про то что некоторое поведение конструкции объясняется тем, что происходит на микро уровне, т.е на уровне молекул.
Лазать туда надо довольно редко. Обычно для практического использования достаточно что-то измерить и сообщить всем значения полученных констант. И никого обычно не смущает, что так называемых констант, т.е чего-то по названию постоянного может быть больше одной.
Вот например, типовой график растяжения стержня висящей на нем нагрузкой:

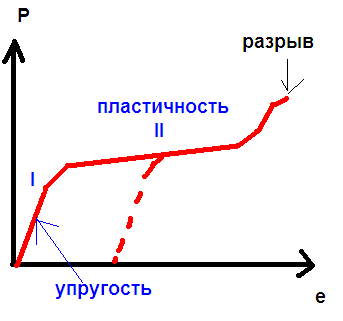
Нагрузка тут  «P», а вызванное ей растяжение «e». До какого-то момента растяжение упруго, т.е если убрать нагрузку деформации исчезнут и все вернётся в исходное состояние. Этот участок на графике вполне прямой, потому запросто можно обзавестись константой, которая связывает нагрузку и деформацию на этом участке и обозвать её модулем упругости или как она там называется. Дело только в том, что работать это всё будет до определённых пределов, т.е до нагрузок при которых нет выхода в диапазон пластичности, при котором  при разгрузке остаются пластические деформации. Видимо, чтобы смешнее было, на этом участке зависимость тоже почти линейна, и потому ничто не мешает обзавестись для него своей константой пластичности.
Теоретически можно было бы сказать, что не константа это вовсе, а функция от деформации и нагрузки. Практически же (для практического применения) оказалось удобнее разделить всё это на два предмета «Теория упругости» и «Теория пластичности». Кроме этого есть так называемая «Физическая механика» в которой многие экспериментально полученные законы объясняются всё тем же движением молекул. В конце концов интересно что же там меняется в материале что вначале он ведёт себя так а потом иначе.
А вчера у меня был… практически конкретный чайник. Для него были получены экспериментальные данные. Думать, что там нарушается закон Фурье нет повода. А вот взять  значение константы – коэффициента теплопроводности из собственного эксперимента я имею полное право. Я же вижу, что тут так, значит так.
Если вернуться к уравнению теплопроводности, то, вроде бы, от досадной странности можно избавится заявив, кто коэффициент теплопроводности вовсе не константа «k», а функция от x, t, т.е k=(x,t).
В выводе уравнения теплопроводности даже ничего особо не поменяется:
http://akostina76.ucoz.ru/blog/2018-03-07-4880

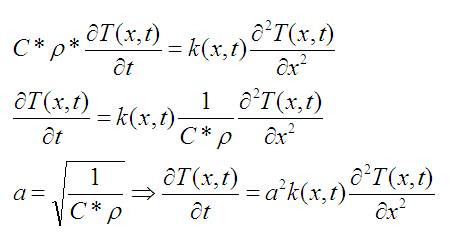
Всё довольно-таки замечательно и очень похоже. Это и есть то самое усложнение уравнения, позволяющее учитывать реальность. Есть только одна проблема: в аналитическом виде это уравнение не решить при всей изворотливости.
А вот численно запросто. Мою лабораторную 1997 года можно взять тут:
https://yadi.sk/d/t8TbZF5VjYddg

За 20 лет не только метод не устарел но и даже программу можно использовать (с).
Одно из уравнений там такое:

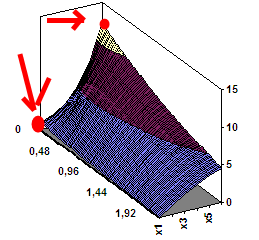
Это как раз вариант с усложнением за счёт ввода функции вместо констант среды. Для данных значений всех функция (включая начальные и граничные условия) результат выглядит так:

… т.е в начальный момент был сильно нагрет один конец стержня (дальний угол) и слабо ближний. Начальная форма нагрева w(x,0) = exp(2.5*x). В нуле это 1, в на другом конце стержня (x=1) это 12. Но уже через две секунды от этого нагрева почти ничего не остаётся. А происходит так потому, что заданы граничные условия, т.е значения температуры на концах, которую можно измерить (w(x=0,t), w(x=1,t)). Интересует, что происходит внутри стержня, куда невозможно залезть с градусником.
Если я задам более покатые функции граничных условий (т.е температуры на концах):.
.т.е напишу так:

… я получу более покатый график:

Единственное за чем надо следить при задании этих условий чтобы функции были равны на концах. В данном случае:

При численном решении тоже происходит отказ от производных как математического понятия. Идёт возврат к понятию приращение функции, т.е отношение изменения значения функции к изменению «x», за который это изменение произошло. Промежутки обычно выбираются достаточно малые (не мои вчерашние 30 секунд), потому с достаточным основанием можно заменять производную тем, что вычислено таким способом:

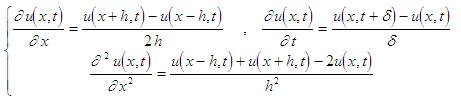
Это засовывается в уравнение любого по сложности вида.  Проделав нехитрые манипуляции можно получить значение функции в точке, ближайшей к начальным и граничным условиям. Там значение функции просто известны как вчера было известно что начальная температура водопроводной воды 10 градусов, а конечная 100. Значение получено, на следующем шаге используется уже оно как будто оно начальное (граничное) условие. Т.е численно, даже особо не напрягаясь, машина находит решение уравнения почти любой сложности.