Производные как инструмент, растяжение стержня и пластины
(Про волновое уравнение в следующей части)
Производная это отношение приращения функции к приращению её аргумента.
Т.е пусть у меня есть некая функция y=f(x):
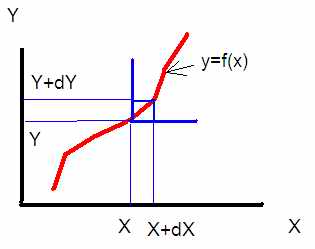
Её производная:
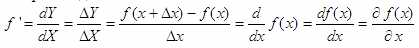
Это всё разные обозначения производной. В школе, вроде, принято обозначать первую производную одном штрихом, т.е y’(x), а вторую двумя штрихами, т.е y’’(x).
Все прочие прописные и строченые d и дельты тоже означают производные. Только в отличие от штрихов такая форма записи позволяет указать переменную дифференцирования. Ведь функции могут быть не только от одного аргумента, а от любого их количества. Может быть например u(x,t), т.е от двух аргументов. Просто штрих не позволит понять, по какому аргументу (x или t) идёт дифференцирование.
На самом деле есть ещё такая запись:
… но крупный вариант позволяет не мельчить буквы, что удобно.
Всё это означает первые и вторые производные, только немного разные.
Первая производная это скорость:
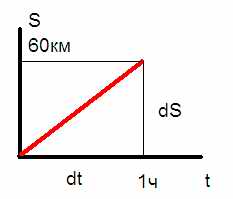
Если здесь поделить приращение функции S (расстояния) на приращение аргумента этой функции t (время), то получится dS/dt=60 км/ч – скорость движения на графике зависимости перемещения от времени, т.е S(t).
А вторая производная это ускорение. Если взять с графика выше все значения скоростей, то получится так:

Чтобы получить вторую производную функции надо взять производную от первой производной, т.е надо проделать те же действия по расчету отношения приращения функции к приращению аргумента. Но тут скорость постоянна, потому dY тождественно (т.е на всем интервале t) равно нулю и вторая производная, она же ускорение, тоже равна нулю.
А вот если взять школьную формулу для перемещения в случае движения с постоянным ускорением, т.е вот это S=a*t*t/2, то это будет график параболы:
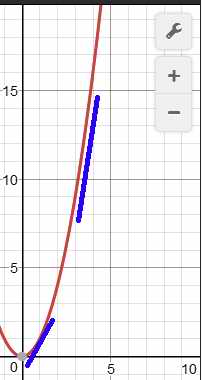
Нарисовать касательные к графику довольно сложно но думаю что и по картинке видно, что их наклон, т.е скорость, т.е первая производная постоянно меняется. Если от этого перемещения нарисовать зависимость скорости от времени, то будет так:

А ускорение тут постоянно. a=dV/dt.
Приращение функции и аргумента, обычно обозначаемые знаком Δ (дельта) это вообще-то ещё не производная. Вот, например:
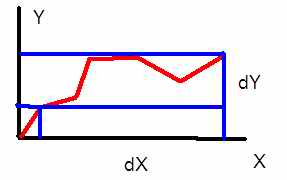
Есть некая функция, в любой её точке можно взять приращения функции и аргумента и поделить одно на другое. Но если я зачем-то считаю производные, то, скорее всего меня интересуют какие-то скорости, а не факт, что при таком делении я получу даже нечто близкое к средней скорости.
Отсюда, от желания узнать точное значение скорости в конкретный момент, появились понятие бесконечно малых промежутков и вся теория бесконечно малых. При расчёте производных считается, что промежуток столь мал, что функцию на этом малом интервале можно заменить прямой и тогда вычисленная по правилам для прямых произвольная даст угол наклона функции в конкретной точке.
Только тогда большое дельта (Δ) становится малым или d. Но на картинках у меня будет dL просто потому, что простенький редактор греческие буквы не рисует.
Стандартная задача механики – растяжение стержня силой F:
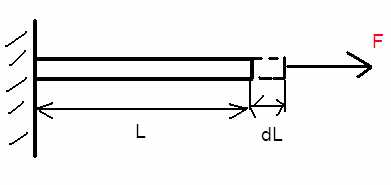
Начальная длина стержня L. Сила растянула его ещё на dL.
Волновое уравнение это скорее про взрыв и ударную волну чем, про струну. Обычно это про волны растяжения и сжатия на всевозможные dL, а не про колебания настоящей струны вверх вниз.
Когда есть более-менее тонкий стержень можно предположить, что сила F всего его растягивает на одинаковую длину.
Но довольно часть бывает что-то такое:

Когда, например, за один конец растягивается резиновая пластинка. Реакцией пластинки на растяжения тут является коллекции напряжений sigma (σ) значения которых разные во всех точках. И потому деформации, растяжения тут тоже не одинаковые.
Но и эта картинка слишком упрощённая. Растягивается и сжимается же не только конец, за который тянут, но и весь кусок материала.
Потому в каждой точке можно взять какой-то бесконечно малый кусок материала:

… и посмотреть, куда он переместился и как продеформировался под действием этой силы. Это уже выход на модель сплошной среды. Весь этот «кусок резины» это сплошная среда с одинаковыми во всех точках свойствами, а деформируется она в разных точках в соответствии с силами, которые в этих точках действуют.
|









