Разбивка на группы (по числовой информации)
Специалистов по статистике не очень много, но благодаря всевозможным опросом значение словосочетания «нерепрезентативная выборка» более или менее известно всем.
Это когда хотели узнать среднее мнение по всей стране, а при сборе информации натолкнулись на необычною группу из тех самых 1000 человек, которые и были опрошены. Необычная группа выдала необычный результат, который не является результатом по всей стране (который пытались определить).
С другой стороны всё ведь зависит от задачи. Средний результат в случае нерепрезентативной выборки не узнать, зато можно порадоваться тому, что удалось обнаружить в обществе некую отдельную группу, у которой, по каким-то причинам вовсе не средние предпочтения.
В эксперименте, описанном тут:
https://akostina76.ucoz.ru/blog/2019-04-04-5756
… одарённые и обычные дети по-разному реагировали на оба типа обучения, показывая различия, позволяющие отнести их к разным группам. У детей ведь, не написано на лбу, какие они. А по этому эксперименту можно это если не узнать точно, то хотя бы предположить с достаточной вероятностью (потому что они по-разному реагируют на внешнее воздействие в виде обучения).
Точно также и агитация за что-то по разному воздействует на разные группы. А результат (предпочтения на выборах) это результат взаимодействия свойств конкретной группы и примерно одинаковой агитации.
Но ведь примерно также можно работать с любой числовой информацией, которая привязана к некому объекту (человека, группе, учреждению, району). Если у него где-то возникла та, а не иная цифра, то что-то можно о нём сказать. Возможно цифра такова, что по этой цифре его можно отнести в некую группу.
В бюджетной базе, например, нет типа учреждения. Потому что никому обычно не надо. А если очень надо, то можно поиграться с подстроками названий, например, выбрав все где есть слово «больница» или «школа».
Я сделала иначе. Я просуммировала расходы по всем учреждениям и для каждого выбрала тот раздел, по которому больше всего было израсходовано денег. Так у меня к детским садам привязался раздел 0701 (Дошкольное образование). Обычно процент именно таких расходов у садов больше 95%.. Как бы ни обозвали этот детский сад, основной раздел расходов точно указывает на то, к какой группе относится это учреждение.
А вот со школами немного интереснее. Для них, естественно, основной раздел 0702. Но этот раздел основной и для районов (потому что деньги школ идут через них). Только для районов расход по разделу 0702 – 30-40%, а для школ обычно от 80%.
Не хочу я название учреждения смотреть. И по сумме бюджета ориентироваться тоже не хочу. А хочу какой-то внятный критерий, который позволит отделить школы от районов только по проценту по основному разделу.
Строго говоря, у меня мало оснований думать, что разброс процентов расходов по основной статье должен укладываться в нормальное распределение. Все-таки велик фактор сознательных решений в этих вопросах. С другой стороны, экономика – результат взаимодействия вполне природной природы и не менее природного человека. А в природе много чего ложится в то самое нормальное распределение.
Кроме того, я всего лишь хочу какой-то инструмент, который позволит мне, по возможности не напрягаясь, упорядочить окружающую информационную реальность. Критерий успеха тут – результат, который меня устроит или нет.
Потому я могу считать разброс цифр нормальным распределением и применить к нему тот метод оценки обычности результата, который применяется для нормальных распределений, т.е Z-оценку отсюда:
https://akostina76.ucoz.ru/blog/2019-04-10-5772
Значение Z-оценки для того что бывает случайно колеблется от -3 до 3. Считается она очень просто:
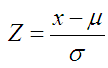
где μ- легко считаемое среднее арифметическое по выборке, σ – стандартное отклонение (СТАНДОТКЛОН() в Excel-е).
По всем учреждениям, у которых основной раздел 0702 у меня получилось среднее значение = 95.51, а стандартное отклонение = 11.83.
Засунув это в формулу для Z, я получаю, что при Z=-3 у меня процент должен быть 60, а при Z=3 – 131.. процент. Это тот случай, когда математический аппарат (в данном случае статистический) не в курсе, что в него засунули проценты. Он в этом видит просто цифры. А ещё ему «объяснили», что они должны лежать на кривой определённого вида (кривая нормального распределения). Вот он и выдал 131%. Но важно не это, а то что районы он успешно отделил от школ. Ещё правда, срезал «СПБ ГКУ ФКСР» с 49.4% и ГБОУ гимназия №7- с 55.72%. Довольно точно.
Немного про всё ту же внутреннюю механику, которая на выходе даёт или не дает что-то похожее на стандартную симметричную горку нормального распределения. Если я буду подбрасывать три игральных кости и нарисую распределение сумм, т.е у меня получится кривая нормального распределения. А если я сделаю третью кость восьмигранной, то получу такое:
|
Сумма
|
Комбинаций
|
|
3
|
1
|
|
4
|
4
|
|
5
|
6
|
|
6
|
10
|
|
7
|
15
|
|
8
|
20
|
|
9
|
25
|
|
10
|
30
|
|
11
|
32
|
|
12
|
32
|
|
13
|
30
|
|
14
|
26
|
|
15
|
21
|
|
16
|
15
|
|
17
|
10
|
|
18
|
6
|
|
19
|
2
|
|
20
|
1
|
Симметрия чуть нарушилось, но понятно, что результат меня не впечатлил. Тогда я заменила 8 (в восьмигранной «кости») на 15. А кто мне запретит придумать фактор, который в вероятностью 1/8 сдвигает результат вправо вдвое сильнее чем обычно в этой системе?
Получилось:

Весь хвост справа состоит из вариантов, в которых есть это 15, т.е из случаев, когда воздействовал этот сильный сдвигающий значение фактор.
В обычной жизни я обычно понятия не имею что вызвало ту или иную форму графика, что привело к образованию длинного хвоста с какой-то стороны. Но могу предположить, что срезая этот хвост Z-оценкой для нормального распределения я срезаю явно необычные объекты в которых явно действовало что-то очень мощное (потому они и стали необычными).
ВВП на душу населения по субъектам (USD по курсу, похоже):
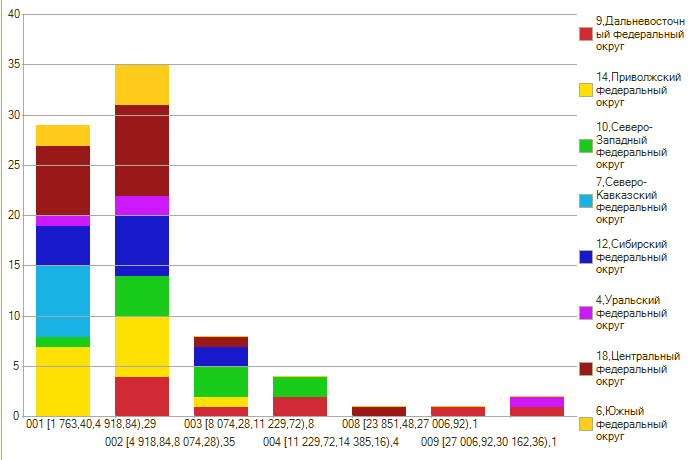
И кого тут считать необычным? Только один правый столбик или два? А может даже три?
Если в рублях, то среднее арифметическое тут 189 161,9, отклонение = 152 218,48. Если я возьму всё тот же диапазон Z-оценки от -3 до 3, то он срежет только Сахалин, Чукотку и Тюмень. Про Тюмень и Сахалин всё понятно (там нефть с газом). Про Чукотку не знаю. Точнее единственное что можно утверждать – очень необычный субъект (случайно такой результат не может быть получен).
Я могу расширить границы странного, поменяв максимум Z-оценки на 1.25. В случае Z-оценок это означает, что вероятность такой случайности 10%. Тогда в компанию необычных попадёт ещё Москва с её мощным столичным фактором.
Следующая группа с вдвое меньшими значениям:

Вообще-то, никто не запрещает мне считать необычными 1, 2 или 3 самых крайних значения. Я как раз и придумываю сейчас критерий необычности, потому могу выбрать любой. Но, по-моему если задаться диапазоном Z-оценок это будет лучше. С потолка в этом случае будет взята нормальность распределения и вероятность случайности, которая всё ещё считается случайностью. Но зато я хоть точно знаю, что именно я беру с потолка и есть хоть какое-то обоснование необычности. При том что крайнее значение 0.919, если остальные 0.92 – вряд ли повод обращать внимание на это значение в этой выборке.
|









