Решение уравнения теплопроводности (2)

В результат всех этих манипуляций:
http://akostina76.ucoz.ru/blog/2018-03-09-4885
… у меня возник определённый интеграл такого вида:

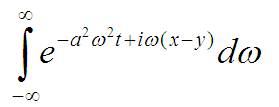
Вычисление интегралов это отдельная вычислительная задача со своим набором инструментов:
https://www.matburo.ru/ex_ma.php?p1=maint

Конкретно здесь (в числе прочего, чуть дальше) будет использован метод замены переменной, про который тут:
https://www.matburo.ru/Examples/Files/NInt5.pdf

Для начала про то, на что эта штука похожа. А похожа она на вот это:

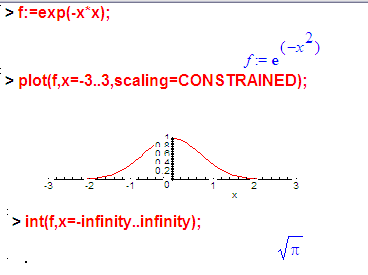
Не смотря на бесконечный промежуток интегрирования, площадь под таким графиком равна квадратному корню из Пи.
Функция может быть чуть-чуть другая. Например, она может быть сдвинута вправо:

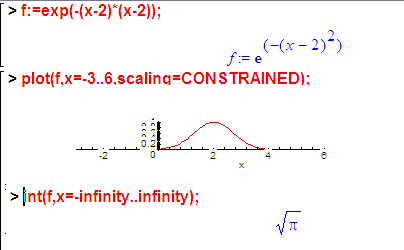
Площадь под таким графиком никак не поменяется.
А вот если функцию сжать коэффициентом при x, то площадь уменьшится в соответствии со значением этого коэффициента:

… но базовый для такого вида функции корень из Пи в значении всё равно останется.
Есть надежда, что и полученный интеграл удастся привести к всё тому же корню из Пи, выдернув из него всё остальное (за знак интегрирования)  в качестве коэффициента.
Разбираю аргумент экспоненты. Первое, что делаю – выдергиваю а скобку минус:

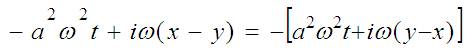
Привести я это всё хочу к виду:

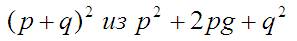
Cразу видно что у меня тут будет «p» и довольно легко вычислить, чем будет «q» :

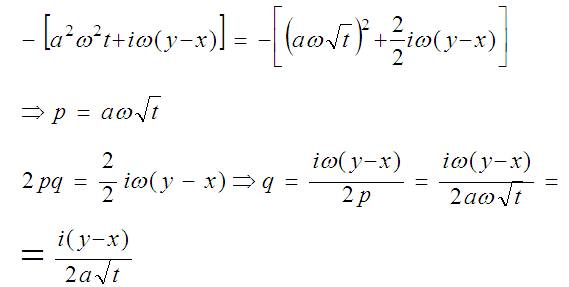
Квадрат этого недостающего q можно добавить и вычесть. От этого выражение никак не поменяется:

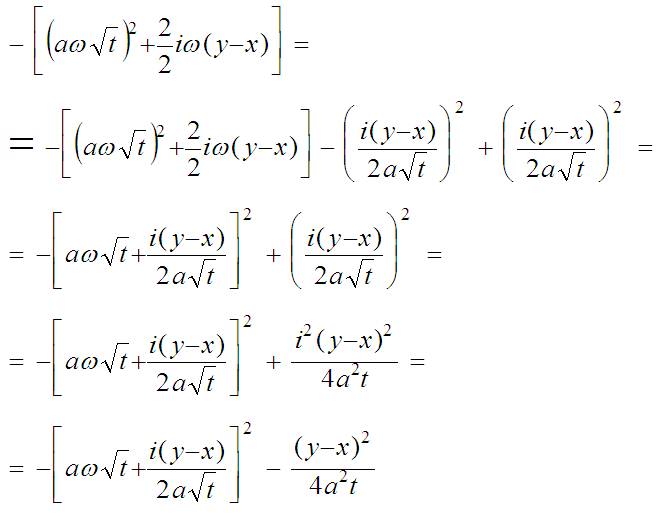
То, что хотелось, получено. Самое время вспомнить, что это не просто так выражение, а аргумент экспоненты в интеграле, а то, что вычитается не зависит от ω, по которому идёт интегрирование. Значит его можно вынести за знак интеграла:

\
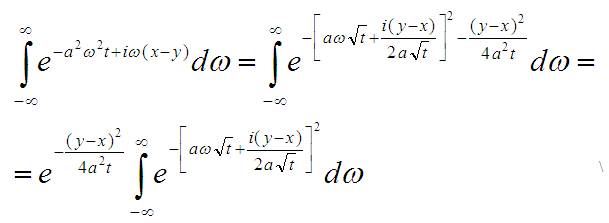Теперь можно сделать в интеграле ту самую замену переменной. Делать её надо не только в подынтегральном выражение, но в дифференциале dω:

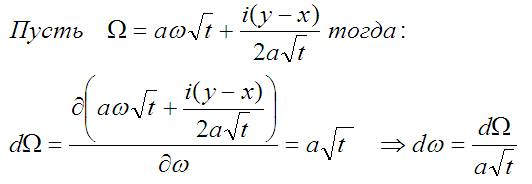
Если подставить всё это в интеграл, то получается так:

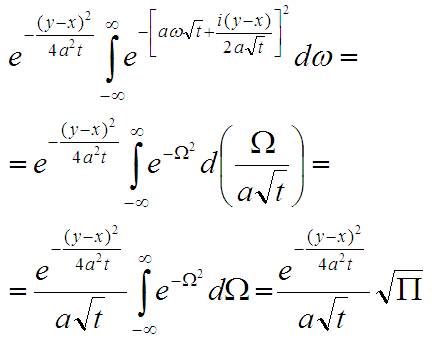
В результате всех этих манипуляций у меня получился тот самый интеграл, значение которого известно и равно корню из Пи.
Интеграл по ω исчез. Вместо него возникло вполне определенное значение. Точнее возникла функция, ведь переменная «y» от оставшегося интеграла никуда не делась. И никуда не делись x, t – аргументы искомой функции температуры u(x,t).
Если подставить полученное в выражение для u(x,t)  предыдущего текста:
http://akostina76.ucoz.ru/blog/2018-03-09-4885
… то получится так:

Под интегралом логично оставить только то, что зависит от «y». Остальное можно из-под него вынести и получить наконец интересующее решение u(x,t) уравнения теплопроводности с известным начальным условием u(x,t=0)=φ(x):