Решение волнового уравнений методом Фурье

Тут:
http://akostina76.ucoz.ru/blog/2017-02-12-3846

..получено решение волнового уравнений при заданных начальных форме и скорости. Всё это конечно хорошо, но к сожалению в решении никак не заданы условия на концах, например, конечной струны длины L. Поэтом полученный вариант решения вовсе не гарантирует что конкретный объект – струна не начнёт колебаться вся целиком, включая закрепленные в реальности концы.
Потому хотелось бы какое-то решение в котором эти граничные условиях (т.е условия на концах струны – границах объекта) уже как-то учтены. Чаще всего надо что-то конкретное, а самое частое из конкретного это та самая струна. у которой смещение на концах строго нулевое.
Запись постановки задачи целиком:

Можно попытаться найти решение u(x,t) = X(x)*T(t), т.е в виде произведения двух функций при этом первая зависит только от координаты, а вторая только от времени. Никто, конечно, не гарантирует, что из этого что-то получится. Случаи, когда из такого во многом метода тыка что-то получается попадают в учебник. Другие варианты остаются на бумаге. Поскольку идёт процесс поиска, то никто не запрещает предположить, что решение имеет указанный вид. А вдруг?
Предложенный вариант подставляется в волновое уравнение:

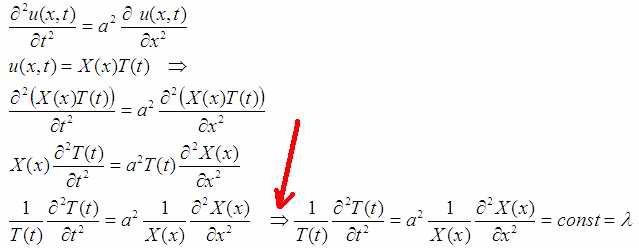
Вначале дифференцирование, потом перегонка функций в другую часть равенства. Спорный и нетривиальный тут только последний вывод. После всех операций слева остались только функции, зависящие от «t», а справа только функции зависящие от «x». И эти вещи равны друг другу. Так может быть только если и то и другое – константа. В противном случае функции, как и полается функциям, менялись бы с изменением аргумента (x или t) и их равенство в какой-то момент исчезло бы.
Одно уравнение разваливается в систему из двух уравнений, а граничные условия очевидно становятся граничными условиями функции X(x):

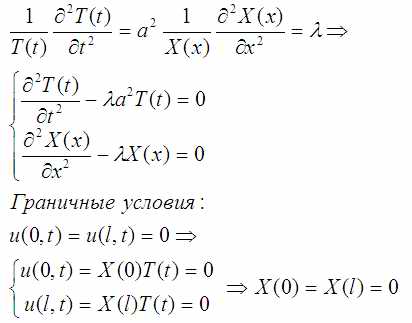
Неплохо бы понять, что за λ такая.
В системе выше возникло два дифференциальных уравнения вида g’’(x)-C*g(x)=0
Уравнения такого типа легко решаются. При положительной константе C неизвестная функция экспонента, а при отрицательной синус, косинус либо их сумма.
Пусть у меня уравнение:
g’’(x)-g(x)=0
Подставлю в него экспоненту:

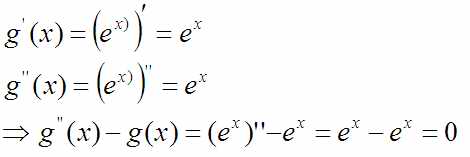
… подходит.
Пусть у меня константа C отрицательная, что означает, что уравнение будет примерно таким:
g’’(x)+g(x)=0
Засуну в него, например, косинус:
http://nice-diplom.ru/templates/blue/images/img/form_30.GIF

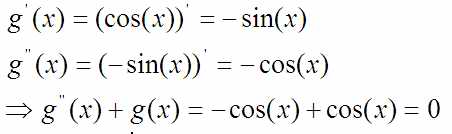
… тоже подходит.
Экспонента это очень быстро растущая функция:

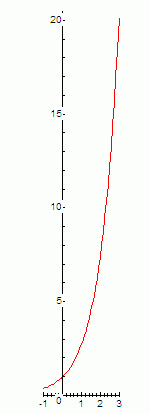
… а синус и косинус это болтающиеся в диапазоне от -1 до 1 волны, т.е видно, что с изменением знака λ принципиально меняется само поведение решения. Но пока нигде не написаны не только конкретные возможные значения этого λ но и даже его знак.
Дальнейший анализ позволит увидеть, что λ в случае решения волнового уравнения с такими граничными условиями обязано быть отрицательным.
Но пусть оно положительно, т.е λ>0. Полный, а не методо-тыковый вид решения уравнения X’’(x)-λX(x)=0 имеет вид:

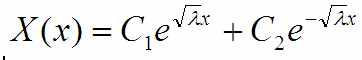
… где C1,C2 – константы, которые полагается определять из граничных условий.
Подставлю в полученное решение граничные условия:


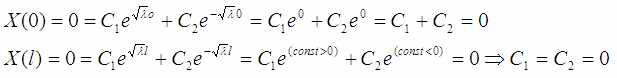
Граничные условия выполняются только если константы равны нулю потому что эти экспоненты выглядят так:

… и сделать их сумму нулём можно только обнулив оба коэффициента.
Значит и решение тождественно равно нулю. А значит и вариант λ>0 надо отбросить как невозможный.
Примерно также можно доказать, что нулём λ тоже быть не может.
Остаётся понять, что будет при λ<0. Прочие варианты отброшены, но отрицательных значений ещё бесконечно много, а решение хотелось бы одно и вполне конкретное.
Общее решение дифференциального уравнения при λ<0 имеет вид:

Сюда точно также подставляются граничные условия:

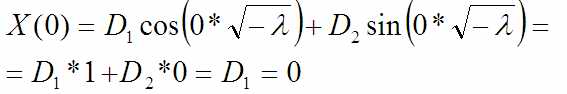
т.е первое граничное условие (u(0,t)=0) обнулило первую константу. От решения остался синус, а от граничных условий – условие u(l,t)=0:

Я не могу обнулить константу D2 для выполнения граничного условия потому что тогда у меня и на этом диапазоне λ получится тождественный ноль. Но по счастью нулём периодически становится и синус:

Достаточно чтобы его аргумент был кратным числу Пи.
Это условие ещё снижает количество возможных значения λ, хотя их всё ещё остаётся бесконечно много, потому, что n=0,1,2,3 и т.д т.е любое целое число. Но всё-таки это меньше чем все возможные отрицательные числа. 
На данный момент возможные решение для X(x) можно записать так:

Этих решений бесконечно много (для всех n=0,1,2…) и во всех в них неизвестные, т.е ниоткуда не определённые константы Dn. Все они никак не противоречат волновому уравнению и заданным граничным условиям. Подставить можно что угодно, всё подойдёт.
Выше была система из двух дифференциальных уравнений. Надо подставить всё, полученное для X(x) в уравнение для T(t):


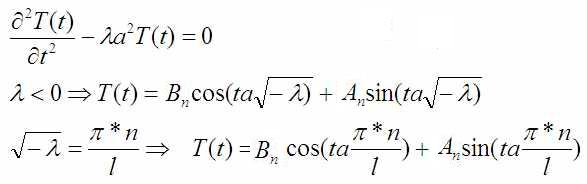
Никакие граничные условия у меня не обнуляли никакие константы потому тут есть и синус и косинус и своя «коллекция» неизвестных констант An и Bn.
Все полученные Xn(x) и Tn(t) можно перемножать между собой. Эти бесконечные комбинации будут сооружать некие решения:

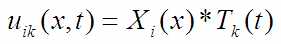
… удовлетворяющие всему, что было учтено выше (т.е волновому уравнению и граничным условиям).
А можно написать довольно смело, хоть и правильно:

Ведь если все отдельные слагаемые удовлетворяют всем условиям, то и их бесконечная сумма никуда не денется, т. е и она (а она тут и написана)  тоже будет решением уравнения.
Осталось то, что ешё нигде не было задействовано. Это начальные условия. Подстановка t=0 в полученное решение обнулит синус и сделает единицей косинус:

 
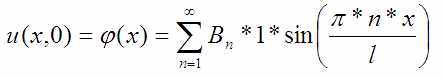
Второе начальное условие:

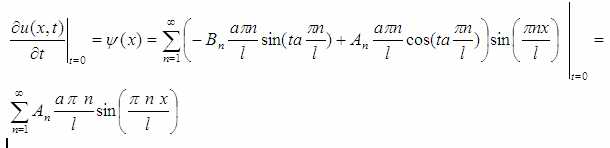
А эти суммы чудесным образом совпадают с разложением функция φ(x) и ψ(x) в ряд Фурье, про который было тут:
http://akostina76.ucoz.ru/blog/2017-02-22-3882

В рядах Фурье функция представляется как бесконечная сумма синусов с какими-то константами – коэффициентами. Приравняв значения коэффициентов оттуда и коэффициенты при синусах и косинусах, поученные из начальных условий можно получить значения этих констант и итоговый вид решения: