Типы частотных распределений

При вычислении процента из двух цифр получается одна, т.е теряется половина (!) информации. Но в некоторых случаях удобно смотреть и сравнивать именно проценты.
Коэффициент корреляции делает из двух (иногда длинных) столбцов цифр одну цифру. Но он же позволяет не рассматривать два графика из 200 цифр (который, к тому же, ни в какой экране не влезет) а получить информацию о синхронности изменений (которая может зачем-то быть интересна и нужна).
Тип распределения позволяет заменить словом-названием целый график. А если к нему добавить ещё пару цифр, то это может уточнить информацию, не сильно увеличив её количество.
Например, такой график можно заменить двумя цифрами:

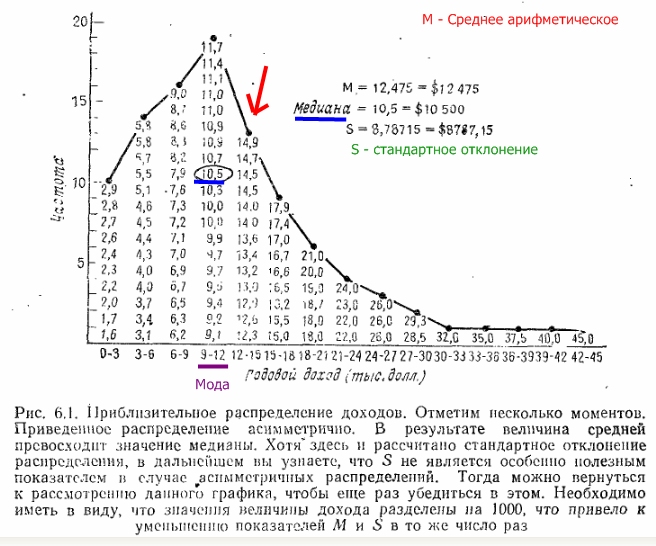
… модой (самым частым значением) и средним арифметическим. Вместо моды можно использовать медиану – среднее значение из всех (если всего цифр 100, то медианна будет 50-м в сортировке по возрастанию).  Если среднее арифметическое больше моды, то, не видя график, можно сказать, что график – это горка с более длинным правым хвостом. В графике в данном случае 100 цифр. Можно их глазами просматривать, можно  график нарисовать. Но иногда можно обойтись несколькими цифрами. Что-то типа снижения трафика – нагрузки на сеть. По типу распределения «гора» мозг сам способен нарисовать «гору» (без передачи этой информации).
Нашла коллекцию типов распределения:
https://habr.com/ru/post/331060/

Это не единственный вариант, зато тут много названий которые можно искать. Ещё тут про них:
http://sixsigmaonline.ru/baza-znanij/22-1-0-229
Порядок будет такой, в каком они мне будут случайным образом попадаться:
ВВП на душу населения за 2012 год:

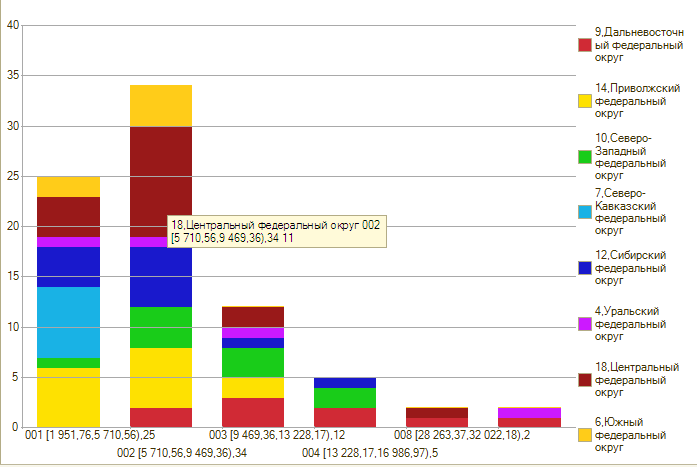
А факторах тут немного не к месту, но всё-таки замечу что «вершину горы» создал Центральный федеральный округ. Точно также картину любого частотного распределения создаёт множество каких-то известных или неизвестных факторов.
По виду это распределение больше всего похоже на «Отрицательное биномиальное распределение». Хотя то тому же виду подойдут и хи-квадрат и гамма-распределение:
http://statsoft.ru/home/textbook/modules/stdistrfit.html

Может, даже, логарифмическое нормальное. Все они похожи не горку с длинны правым хвостом.
Доходы бюджетов, всего:

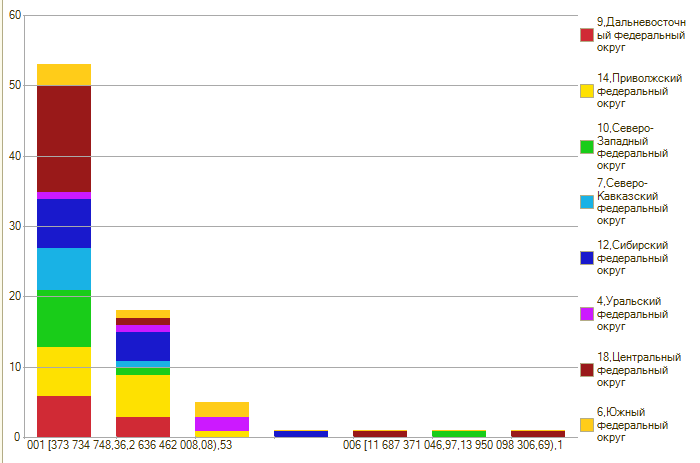
Скорость убывания функции заставляет вспомнить экспоненту с отрицательным аргументом. Экспоненциальное распределение, скорее всего.
Вчерашний пример бимодальной (с двумя вершинами) функции (автомобили на 1000 человек):

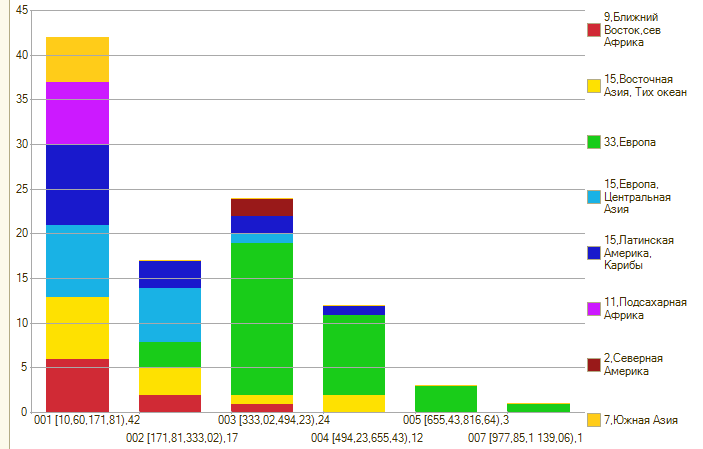
Естественный вид экспоненты тут нарушен фактором в виде богатой и оснащённой автотранспортом  Европы.
Процент городского населения по всем странам мира:

… сойдёт за дискретное равномерное (однородное) распределение (uniform). Это соотношение (по всему миру) есть на любой вкус. И стран с разным соотношениями (городских и сельских жителей) примерно одинаковое количество. 
Ценам на бензин (Fuel prices refer to the pump prices of the most widely sold grade of gasoline. Prices have been converted from the local currency to U.S. dollars.) естественно было бы быть нормальным распределением:

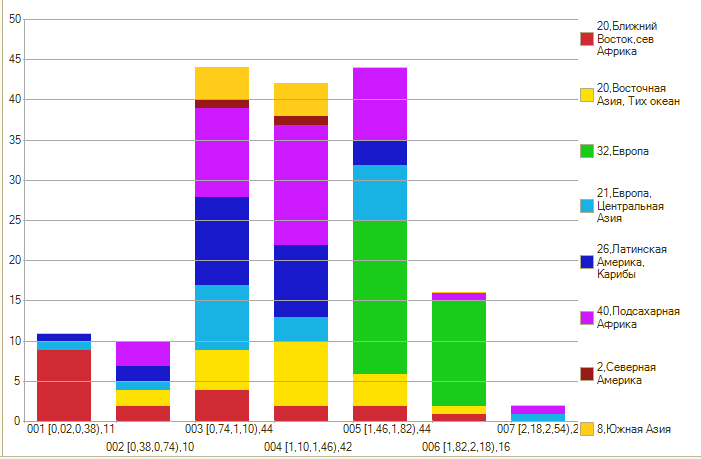
Примерно так оно и есть если не считать Ближний Восток где цены для своих граждан, так понимаю, ниже:

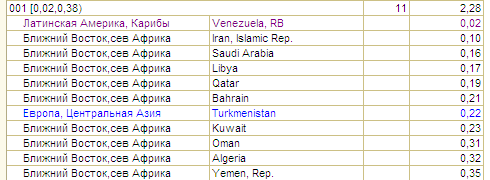
Возрастающая функция (бэта) это то, что есть почти у всех. Например, «Иммунизация, кори (% детей в возрасте от 12-23 месяцев)»:

Интересно, что много каких-то денег у многих не бывает. Такая картинка может возникнуть скорее вопреки этой естественной картине убывания. В данном случае было принято волевое решение сделать так чтобы привиты были почти все во всём мире.  
У меня в базе нет привязки типа распределения (т.е закона, по которому меняются частоты) к параметру. Потом я так и не смогла быстро найти более менее подходящие для иллюстрации «столбики» по краям диапазона.
Законы тут, кроме всего, не всеобщие, потому что по всему миру процент городского населения – равномерное распределение, а по нам – несимметричная горка:
https://akostina76.ucoz.ru/blog/2019-04-10-5772

Но, всё-таки, наверное есть и общие закономерности, которые являются следствием »внутренней механики», которая формирует частотную характеристику для определённого параметра.
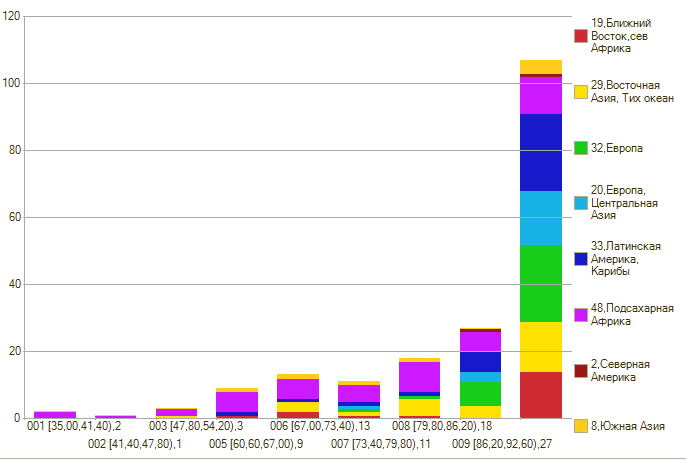
Два столбика по краям наводят на мысль об инвестициях, при которых половине почти ничего не дали, а половине дали довольно много (на закупку какого-то оборудования, например). За неимением лучшего, что быстро можно найти, распределение штук учреждений по суммам экономической статьи 310

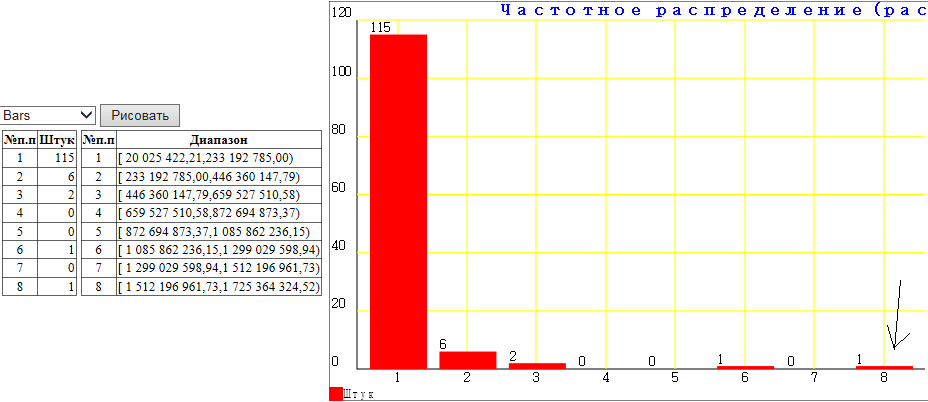
Тут выбраны не все учреждения, а с суммой по 310 статье больше 20 млн. То тем, у которых меньше – обычная убывающая экспонента. А отдельно от всех находятся «Водоканал» и «Мариинская больница»:

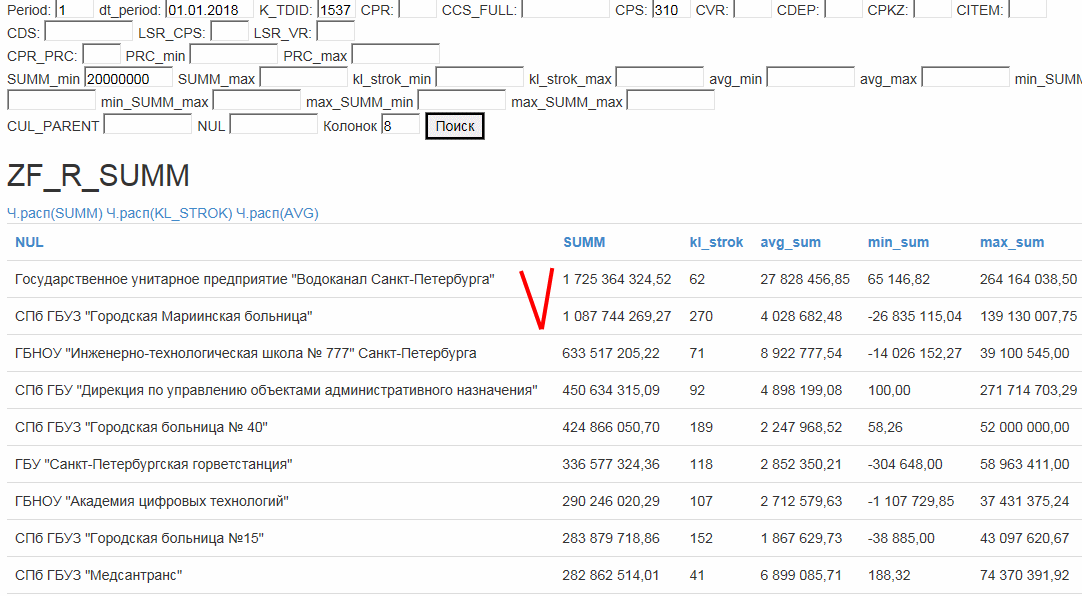
туда какое-то оборудование закупили.