Вывод решения волнового уравнения

Добыто тут:
https://drive.google.com/open?id=0B3i2SFYLER0HanRQT0JJOEtESUU
Есть такое волновое уравнение:

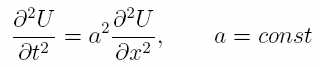
где a – некая константа, не особо важно какая по величине, а U=U(x,t) – функция от координаты x и времени t.
Чтобы решать уравнение с второй производной по времени надо как минимум определить два начальных условия:

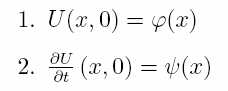
… т.е картину перемещений – деформаций в начальный момент времени U(x,0) (т.е при t=0) и скорость (первая производная) в тот же начальный момент времени.
Дальнейшие действия обычно делаются под девизом «Давайте попробуем, а вдруг что-то хорошее из этого получится.
Вот возникла идея переопределить переменные:

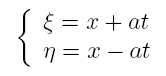
… т.е завести вместо пары x и t пару ζ и η. Такая идея переопределения может и не совсем на пустом месте возникла. Ведь при подборе подошло нечто похожее:

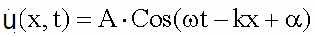
… и экспонента с +kx.
Дальше действует то  самое правило дифференцирования сложной функции, из всё того же математического анализа, который дал таблицу производных.
Производная по времени после переопределения переменных считается по такой формуле:

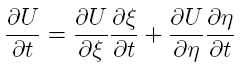
Осталось подставить то, что имеется:

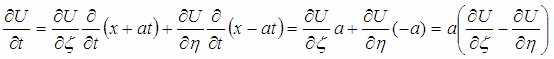
Но ведь в начальном уравнении вторые производные и именно их надо выразить через новые переменные. Вторая производная по t выводится по той же формуле дифференцирования, но применённой не просто к функции, а к её производным по ς и η.
Я их вначале посчитаю отдельно, а потом сложу.
Первое слагаемое:

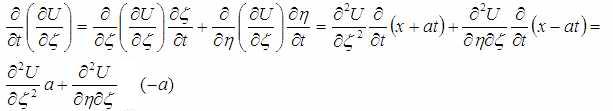
Второе слагаемое:

 

Не смотря на страшненький внешний вид основная сложность тут в том чтобы сделать это аккуратно, т.е не перепутав знаки и не потеряв константы.
Сумма:

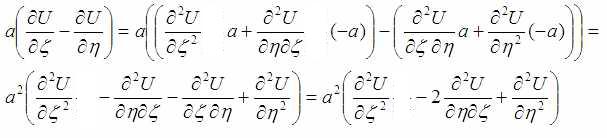
Нарисовав примерно такие же «обои» можно получить вторую производную по x:

Теперь надо это приравнять, составив волновое уравнение с уже новыми переменными:

Довольно логичен вопрос: Куда девалась константа «a» из начального варианта волнового уравнения? От неё можно избавиться, сделав ещё одну замену переменных, т.к при исследовании функции она только мешает (вроде так…).
Уже видно главное. Что-то равно себе же с отрицательным знаком, только если оно равно нулю. Значит:

Это может быть только в случае если U – сумма двух функций от отдельных аргументов, в ней нет функций, связывающих сразу два аргумента:

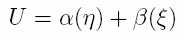
При таком устройстве дифференцирование по одной переменной убьет одну из функций-слагаемых (как константу, не содержащую переменной, по которой дифференцируют), а дифференцирование по второй переменной точно также расправиться со второй функцией, в результате чего и получится тот самый тождественный ноль. 
Искомая функция всё ещё неизвестна, но уже понятно как она устроена. Потому можно вернуться к начальным переменным (воспользовавшись правилом замены переменных выше):

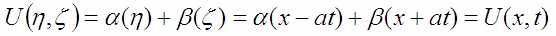
Теперь можно вспомнить начальные условия, т.е условия при t=0 воспользоваться всё тем же правилом дифференцирования сложной функции (дифференцируется и функция и её аргумент, результат перемножается):

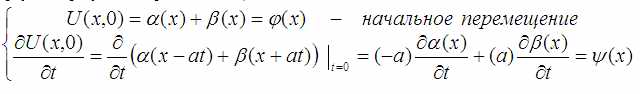
Ничто не мешает продифференцировать первое уравнение по t. Равенство от этого никуда не исчезнет. А ещё его сразу можно умножить на «a». Система уравнений примет такой вид:

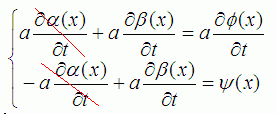
А теперь можно их цинично сложить. Тогда первая функция (α) обнулится и останется такое:

Чтобы из производной β получить искомую функцию надо проинтегрировать правую часть. При этом интеграл от производной это сама функция φ(x) (т.к интегрирование и дифференцирование это обратные операции) , а вот от ψ(x) всё-таки придётся брать интеграл. Будет так:

Если вычесть уравнения, то совершенно аналогично исчезнет функция β и можно будет получить функцию α из того, что осталось. Вместе будет так:

Тут присутствуют две константы C1 и C2 но они обнуляются. А ещё тут интегралы из неопределенных, т.е задающих функцию стали определёнными (от 0 до x) т.е задающими значения функций (площадей под графиками в какой-то точке).
Теперь если это всё просуммировать (т.к U=α+β) и вспомнить, что t не обязано быть равно нулю, то будет так:

или так:

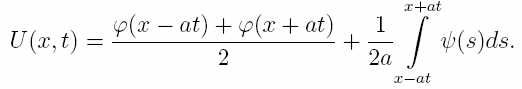
Дальше можно уже играться подставляя конкретные значения начальных условий φ и ψ и рисуя графики того, что получается при таких начальных форме и скорости.