Вывод волнового уравнения из законов Гука и Ньютона

Украдено отсюда:
http://msk.edu.ua/ivk/Fizika/2_kurs/Tushev_Shizika/TUSHEV2/15-3.html
… и изложено своими словами.
Продолжение этого:
http://akostina76.ucoz.ru/blog/2017-02-08-3835

В механике довольно часто места с наиболее большими и даже опасными напряжениями изображаются красным цветом. Вот, например:
http://www.solidworks.com/sw/resources/videos/demo-library-solidworks-simulation.htm

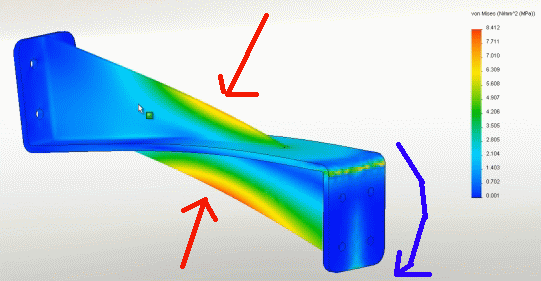
Балка, которую пытаются гнуть имеет, естественно, наибольшие напряжения сверху (напряжения растяжения) и снизу (напряжения сжатия).
Но пусть я хочу как-то визуально отличать напряжения сжатия и растяжения. Пусть напряжения растяжения положительны, а напряжения сжатия отрицательны.
Я, например, буду обозначать максимум напряжений растяжения красным, а близкое к нему фиолетовым.
Максимум напряжений сжатия я нарисую желтым, а подход к нему оранжевым.
Ноль, т.е места где нет напряжений будет синим, а промежутки зелёными и голубыми.
Тогда если вдруг по стрежню пойдут переменные деформации и напряжения он будет выглядеть так:

Т.е есть некая загадочная сила F, которая ухитрилась создать в стержне такую картину напряжений (то сжатие, то растяжение).
При этом цветную раскраску используют всё-таки редко. Значительно чаще и для внутренних напряжений и для созданных ими деформация используются обычные графики.
Те же напряжения на графике выглядели бы так:

Мне лень было рисовать гладкий синус, но можно было изобразить и его. Но это всего лишь график внутренних напряжений, которые то положительны, то отрицательны, а не форма, которую принимает струна или стержень.
При этом понятно, что если где-то возникло сжатие, то рядом должно быть растяжение. Потому, что если его там нет, значит там уже что-то порвалось.
Волновое уравнение в общем случае имеет такой вид:


Где u(x,t) – это перемещения в точке x в момент времени t. Струна – стержень лежит вдоль оси X, а раз по нему идёт волна, то перемещения разные для всех x стержня. А раз процесс динамический, т.е меняющийся во времени, то и от времени t эти перемещения зависят.
В волновом уравнении приравниваются вторые производные по времени и координате. Выводится уравнение из законов Гука и Ньютона.
Общий вид закона Гука:

и относится он к такой картинке:

Из этого закона сразу видно, почему на разноцветных картинках у меня было про напряжения, а в волновом уравнении напряжения вдруг превратились в перемещения – деформации. Между этими параметрами линейная зависимость, константа – коэффициент упругости k.
В законе Гука хоть как-то присутствует изменение длины, т.е dX.
Второй закон Ньютона включает в себя вторую производную по времени:

У меня тут перемещение обозначено привычным S, а не u, но важна не буква, а наличие второй производной по времени.
Сила F одна и та же. Приравниванием этих двух уравнений и будет получено волновое уравнение.
Длинная струна одномерна, т.е это что-то очень тонкое и очень длинное, но поскольку в ней все меняется при изменении X то и в ней как в широкой резиновой пластинке логично вырезать маленький цилиндр и посмотреть как перемещался и деформировался именно он:

Под действием силы F он во-первых весь куда-то переместился (из-за деформация окружающих кусков), во-вторых, почти наверняка растянулся.
Здесь выбран кусок цилиндрической формы видимо потому, что он ассоциируется со струной (которая тоже – всего лишь название одномерной модели; той в которой всё деформируется вдоль одной переменной x). С таким же успехом можно было представить брусок или кусок шестигранного карандаша.
Когда примерно то же самое выводится для жидкости, которая может течь в любом направлении обычно говорят об бесконечно малом объеме произвольной формы:

Дальше я буду рисовать не объемную картинку, а вид сбоку:

Т.е кусок весь переместился на u(x) и продеформировался на Δu(x)
Эта картинка очень похожа на нарисованный выше стрежень, продеформированный на ΔL.
Закон Гука можно записать не только через F и ΔL но и через придуманные параметры напряжений σ и деформаций ε.
Их просто придумали и определили так:

Здесь S – площадь поперечного сечения стержня – струны – цилиндра.
Но вырезанный из струны цилиндр очень похож на стержень, а деформацию ε в нем логично обозначить так:

… т.е тоже отношение изменения длины к начальной длине. В случае бесконечно малых,
 а тут именно этот случай отношение приращений Δ становится первой производной.
Закон Гука, записанный через σ и ε имеет вид:
σ = E ε

Если подставить эти новые придуманные параметры в начальный вариант закона Гука, то будет так:

Т.е E, как и k это тоже константа модели. Просто кроме коэффициента упругости в неё вошли ещё геометрические размеры стержня – цилиндра L и S.
С деформацией растягиваемого цилиндра уже понятно. Из-за малости объема её можно считать первой производной от координаты x:

Но ведь цилиндр на самом деле растягивает пара сил, причем противоположных по направлению:

А значит суммарная действующая сила, которая вызвала деформации это их разность:
F = F(x+Δx) – F(x)
Можно произвести замену переменных, воспользовавшись определением σ:

А теперь сюда можно подставить закон Гука записанный через σ и ε:

А теперь самое время вспомнить, что ε это первая производная от u(x). Кроме этого все это надо поделить и умножить на ΔX. Это одновременное деление с умножение даёт умножение на 1 т.е ничего не меняет, но оно позволяет получить долгожданную вторую производную:

Первая производная это всего лишь некая функция потому она дифференцируется и вычисляется по приращениям точно также как и все остальные.
Осталось вспомнить, что закон Ньютона это F= m*a,  а масса m это произведение плотности ρ, площади цилиндра S и его длины ΔX.
Подставив все это и приравняв, получается так:

Вот и всё. Это и есть классический вариант волнового уравнения, который был нарисован в начале текста.
Дальше придётся его как-то решать.