Методы расчёта

Здесь:
http://akostina76.ucoz.ru/blog/2018-03-10-4886

… решение уравнение теплопроводности. Хоть как-то его удалось решить благодаря необычным свойствам… комплексных чисел. Напомню, что там при решении используется эта формула:

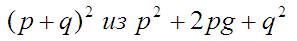
При любых значениях p и  q никого минуса перед q*q быть не может если оставаться в «мире» обычных чисел потому что, что угодно в квадрате положительное.
А окружающая реальность, т.е физические законы сохранения и потери тепла, подкинула мне уравнение,  где вместо столь нужного мне плюса стоит минус. И потому я к виду (p+q)^2  это выражение преобразовать не могу.
С другой стороны я знаю школьное, что корни из отрицательных числе извлекать низяяяя.
Утверждать, что именно уравнение теплопроводности привело к тому, что придумали комплексные числа, т.е числа квадрат которых отрицателен, я не буду. Скорее всего к этой проблеме подошли сразу с нескольких задач, так и придумалось решение (в виде пространства комплексных чисел).
Метод вполне естественен для математического анализа. Напомню всё тот же первый абзац:
 
Что значит «нельзя извлекать корень из отрицательного числа»?! Из положительного, вообще-то тоже нельзя. Не существует этих корней в пространстве дробей (т.е p/q). А в пространстве целых чисел нет даже половин яблок из арифметики для начальных классов  Но яблоки-то есть!
Тут надо очередной раз написать, что математический анализ это не наука, а аппарат. Это такой компьютер для времён когда не придумали ещё даже калькулятора. Потому очень важно иметь решение в аналитическом виде, в которое достаточно подставить либо свои (данные конкретной задачей) цифры или даже функции (начальные и граничные условия при решении дифференциального уравнения).  Без этого ничего не сделать потому что единственный инструмент – карандаш.
Нерешённых задач в этом анализе сколько угодно. Сразу вспоминаются хотя бы неберущиеся интегралы. Напомню, что интеграл это величина площади под графиком. Функция не виновата что не существует другой функции, чья производная ей равна. И площадь под такой функцией есть (как и под любой другой). А вот математического аппарата, позволяющего её быстро посчитать, не придумано. 
Функций, для которых интегралы считаются мизерно мало. Интегралы и весь инструментарий с ними связанный от этого не перестаёт быть выдающимся изобретением. Имеет смысл вспомнить, что придумывали его примерно тогда же когда из пушек вылетали круглые ядра, траектории которых надо было как-то обсчитывать. Тогда этих возможностей хватало. А сейчас люди хотят знать, какой минимальной толщины может быть деталь сложной формы, чтобы она отработала свой гарантийный срок и не сломалась. Лет 20 назад было большим достижением то, что любую накладную можно почти мгновенно найти по номеру не роясь в бумажках (потому что совсем недавно и этого не было). А сейчас этого как-то мало потому я пишу о списках проводок, регистрах и прочих внутренних инструментах придуманных когда возросли и запросы и технические возможности.
Довольно естественно (с учетом истории) попытаться придумать для таких неберущихся интегралов пространство каких-нибудь дополненных функций, с которыми можно столь же просто работать и получать те самые площади под графиками.  Но этого, пока, никто не делает потому что основным методом решения стала машина.
Я не знаю когда математическая физика (с тремя основными уравнениями) стала отдельным предметом, но этот предмет уже ориентирован на машинное получение информации. Там возникает определение корректно поставленной задачи. Перед тем как что-то решать (засовывать в машину) надо убедиться, что решение существует, единственно и устойчиво.
Машина может считать что угодно и как угодно. Можно, например, искать корни квадратного уравнения перебором всех чисел от -10 000 до + 10 000 с шагом 0.01. Это очень… плохой метод, но и такое сойдёт если ничего другого не придумать.
Напомню, что корни квадратного уравнения это точки пересечения параболы с горизонтальной осью:

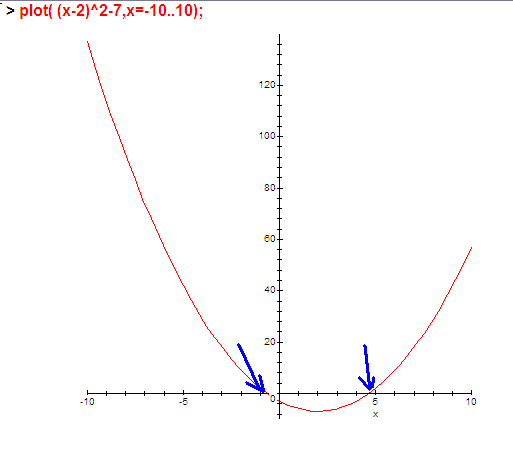
Парабола это функция с «рогами» либо вверх либо вниз и (в общем случае) вовсе не обязанная пересекать эту ось (она вся может быть выше или ниже её). Если я засовываю поиск корней в машину и машина перебрав все варианты не нашла решение это неприятно но хотя бы понятно. А если она нашла не два корня а четыре?..  Это означает, что засунутое в неё не было параболой. Я думаю, что это парабола но я ошибаюсь. В постановке задачи, т.е в попытке придумать модель какого-то процесса допущена какая-то ошибка. Если я пытаюсь описывать маятник а в решении у меня не синус а вылет на орбиту с всё возрастающей скоростью то у меня получилось описание ракеты причём довольно необычной.  Если получать решение в аналитическом виде это не очень важно потому что все эти ошибки где-нибудь да вылезут в виде очевидных нестыковок с реальностью. А машина, в которую засунули непонятно что, выдаст ещё более непонятно что.  И почти наверняка оно будет не научным открытием а просто полным бредом полученным по всем правилам но с какой-то мелкой вкравшейся ошибкой (типа забытого знака). 
Чуть более сложный пример того, что бывает, если что-то забыли пририсовать в постановке задачи:
http://akostina76.ucoz.ru/blog/2017-02-11-3842
Что касается конфликта Келдыша и Устинова то суть я, естественно, не знаю. Сказано, что Келдыш хотел уделять больше внимания теории а не практике. Деление на теорию и практику ни то чтобы условно. Скорее слово «теория» немного не подходит. Можно назвать математический анализ теорией потому что сам по себе он не даёт конкретных результатов. Но назвать его и прочие подобные вещи необходимым инструментарием, неверное,  корректнее.
Придумывать и делать инструменты тоже периодически надо. Можно и без них. Но если резать доску под углом без стусла:

… будет либо медленно либо неаккуратно.  Иногда надо останавливаться и чуть-чуть думать как иначе что-то сделать. Допускаю, что там что-то такое было.
Возвращаюсь к математическому анализу. Я не знаю, чем сейчас занимается их передний край, так сказать. Теорема Ферма это интересно скорее как то, что давно висело вопросом и то, что всё-таки надо было сделать (т.е как-то неприлично было без этого). Последнее известное мне как полезное в хозяйстве это те самые комплексные числа и их многочисленные (включая неожиданные) применения.
Вычисление интегралов с помощью суммы вычетов:
http://mathhelpplanet.com/static.php?p=vychisleniye-integralov-s-pomoshchyu-vychetov

… это, по-моему, тот случай когда ничто не предвещало))).
Потому я не думаю, что учебник Фихтенгольца это такой уж вчерашний день. В таких предметах главное понятное объяснение, т.е текст между формулами. Сразу напишу, что лично я не читала, но подозреваю, что это лучше многих других вариантов. Для пошевелить мозгами наверное, сгодится.
Ещё один «кусок» этой темы – задачи. При всей парадоксальности этого факта, практика математического анализа с теорией по духу, метод и прочему почти не связаны. Это отдельно и больше всего похоже на кроссворд, когда руки и голова чем-то заняты.
Вот про решение пределов:
https://www.matburo.ru/ex_ma.php?p1=mapred

… а это про интегрирование:
https://www.matburo.ru/ex_ma.php?p1=maint

При наличии Maple занятие дурное, но для проиграться самое то (если это сдавать никуда не надо).
Задачник вроде этот был:
https://drive.google.com/file/d/1uZMuoSRXeY6cC68VYigxM86_QrT31rJo/view?usp=sharing

p/s
Интеграл вычетами там же:
https://www.matburo.ru/ex_ma.php?p1=matfkp
p/p/s
Плохой опыт: Физику читал Гунько. Ему, по-моему, было плевать слышно ли то, что он говорит и видно ли то, что он пишет. Но это можно было потом разобрать и понять. Несколько лекций читал не помню кто, довольно молодой. Он вообще задиктовывал и ждал, когда все запишут. Мне потом, по-моему, так и не так и не удалось понять что он пытался сказать. Так что новее не значит лучше, не все эксперименты в этом хороши.