Начальные условия волнового уравнения на примере косинуса
Тут:
http://akostina76.ucoz.ru/blog/2017-02-11-3842
… быстро придумалось решение волнового уравнения как, например:
u(x,t) = cos(6*t-2*x)
Константа «a» для этого уравнения = 6/2=3.
Взяв начальные значения из этого решения можно увидеть какой вклад каждое из них вносит в итоговую волну.
Отсюда:
http://akostina76.ucoz.ru/blog/2017-02-12-3846

и:

Осталось всё аккуратно посчитать для конкретного косинуса:
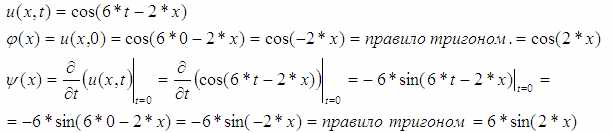
Подстановка «a», вычисление интеграла:
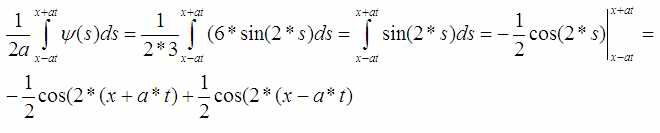
Всё вместе:
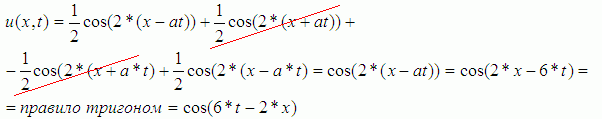
Вывод до начального значения, т.е косинуса тут для проверки.
Интересно то какой вклад в решение дают обе части u(x,t), т.е слагаемые с φ и интеграл с ψ.
Обсчёт всего этого в Maple:

|
u_1(x,t) – функция от φ
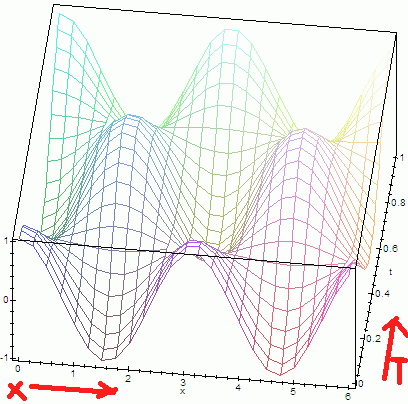
|
u_1(x,t) – функция от ψ

|
Но если их просуммировать то будет ранее полученный вариант:

Лично у меня пространственного воображения не хватает чтобы понять почему вклады начальной формы и начальной скорости такие и как получается что при суммировании выходит такая форма. Вот они вместе, одно приподнято над другим:

Сразу видно насколько сильно поменяется картина если убрать одну из составляющих.
По такому графику, т.е по u(x) при t=0 и 0.05 видно чуть лучше:

За такой маленький промежуток времени вклад u_1() почти не поменялся, а вот вклад скорости – интеграла подрос довольно существенно. Он-то и сдвинул итоговую волну вправо на видимое расстояние. До «впадины» вклад «горба» положительный потому левая часть увеличивается, сдвигая волну вправо. А после «впадины» вклад отрицательный, но это очень удачно сдвигает волну на этом участке тоже вправо.
Три графика:

Все тексты в Maple:
omega:=6:
k:=2:
a:=omega/k:
u_cos:=(x,t)->cos(omega*t-k*x);
fi_t_0:=unapply(u_cos(x,0),x);
psi_t:=unapply(diff(u_cos(x,t),t),x,t);
psi_t_0:=(x)->psi_t(x,0);
u_1:=(x,t)->(fi_t_0(x-a*t)+fi_t_0(x+a*t))/2;
u_2:=(x,t)->int(psi_t_0(s),s=x-a*t..x+a*t)/(2*a);
u:=(x,t)->u_1(x,t)+u_2(x,t);
plot3d(u(x,t),x=0..6,t=0..1,axes=boxed);
plot3d(u_1(x,t),x=0..6,t=0..1,axes=boxed);
plot3d(u_2(x,t),x=0..6,t=0..1,axes=boxed);
plot3d({u_1(x,t),2+u_2(x,t),6+u_1(x,t)+u_2(x,t) },x=0..6,t=0..1,axes=boxed);
plot({u_1(x,0),2+u_2(x,0),4+u_1(x,0)+u_2(x,0) ,u_1(x,0.05),2+u_2(x,0.05),4+u_1(x,0.05)+u_2(x,0.05)},x=0..6,axes=boxed);
plot({u_1(x,0),2+u_2(x,0),4+u_1(x,0)+u_2(x,0) ,u_1(x,0.1),2+u_2(x,0.1),4+u_1(x,0.1)+u_2(x,0.1),u_1(x,0.2),2+u_2(x,0.2),4+u_1(x,0.2)+u_2(x,0.2)},x=0..6,axes=boxed);
p/s
Здесь у меня была ошибка:
http://akostina76.ucoz.ru/blog/2017-02-16-3862
Начальной формой в виде синуса функция задаётся с негласным выполнением условий в начале и в конце струны:

(скобка в формуле не там стояла).
Но это скорее везение и тоже своеобразное угадывание – подгонка. В общем случае эти концы запросто могут болтаться, т.к их пока, действительно не закрепили.
|









