Восприятие и обработка информации

У человека от природы есть несколько рецепторов – органов с помощью которых он получает информацию об окружающем мире. Это глаза, уши и пальцы, в которых можно что-то крутить.
Графическое представление информации придумал, если я не ошибаюсь, Декарт. И это удобно. И до сих пор сплошь и рядом используется. Выпушенный из пушки снаряд, например, провисел в воздухе секунду и куда-то упал, а график траектории позволяет навечно указать место, где он был, и показать понятную картинку всем желающим её увидеть.
Но, к сожалению довольно быстро стали возникать задачи, визуализировать которые трудно. Проще простого, например, придумать пятимерное пространство при том, что окружающая реальность трёхмерна.
Здесь, например:

http://akostina76.ucoz.ru/blog/2017-03-15-3952

… у меня сразу возникает 5 факторов, которые могут влиять на сахаристость ягод. Это содержание в почве азота, калия, фосфора, температура и свет. Пусть X1 – азот, X2 – калий, X3 – фосфор, X4 – температура, X5 – свет.
Пусть мне даже экспериментами удалось установить, что искомый сахар можно найти по формуле:

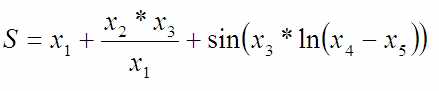
Формулы мне не ставят никаких ограничений, что хочу то и нарисую. А теперь попробуйте изобразить такое на графике. К трехмерному пространству можно добавить цвет точек. А графики можно нарисовать на отдельных страницах книги, добавив ещё одно измерение. Вот и всё, что хоть как-то можно вытащить из бумаги как инструмента передачи информации.
Уже с мгновенными скоростями на траектории снаряда всё не так хорошо, а хотелось бы.
Можно, конечно, взять линейку и измерить угол в конкретной точке по графику:

… но явно же проще и точнее это сделать с помощью формул.
А вот некая функция:

Меня, например, интересует будет ли он на бесконечности меньше 1 или красная линия так и не пересёчёт зелёную. Бесконечность увидеть невозможно, значения функции в ней тем более, и иногда надо знать такие вещи точно.
Или, например, такая функция и меня интересует её интеграл, т.е площадь под графиком:

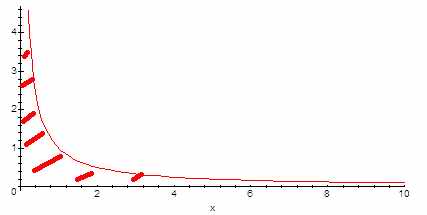
… т.е интересует хотя бы конечная она число или бесконечность. С одной стороны бесконечный период намекает на бесконечную величину площади, но ведь и функция убывает очень быстро. Примерно то же самое происходит у нуля. Быстрый рост функции компенсирован малым диапазоном X, где функции принимают столь большие знамения.
Здесь я писала про Дельта-функцию Дирака:
http://akostina76.ucoz.ru/blog/2017-02-14-3854
… которая в нуле равна бесконечности, но бесконечно малый диапазон возле нуля делает площадь под таким графиком равной единице.
А вот так выглядит график этой интересной функции:

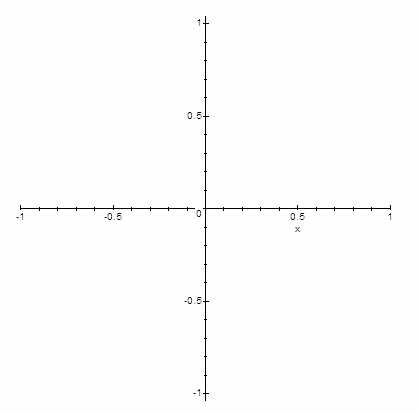
… его вообще не видно, хотя функция там есть. Достаточно взять от неё интеграл на том же диапазоне чтобы убедится, что она там есть:

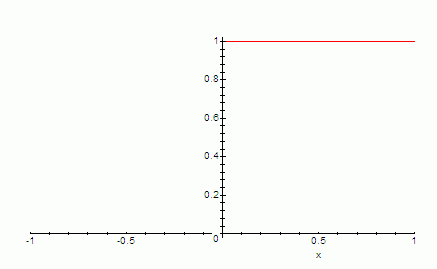
Глаза не работают. Точнее работают, но информации не дают. А бывает хуже, глаза в компании с интуицией могут ошибаться.
Здесь:
http://akostina76.ucoz.ru/blog/2017-03-01-3908

… у меня было два дифференциальных уравнения.
Первое g’’(x)-g(x)=0, второе g’’(x)+g(x)=0. Ведь очень похоже! Изменён только знак перед вторым слагаемым. Логично же и решениям быть хоть как-то но похожими. Но ничего подобного. Трудно, по-моему, придумать что-то более непохожее:

А ведь это не цифры, а поведение какой-то механической системы, которое будет при одном знаке некой константы таким, а при другом этаким.
Но самый показательный пример (потому его очередной раз и вспомню) это отваливающиеся крылья самолётов. Ведь очень хочется при таких проблемах закрепить посильнее переднюю часть крыла, на которую дует. А вот этого-то как раз нельзя делать. Потому, что модель такая:

Это пластина на двух пружинах, обдуваемая потоком воздуха. Большая прочность спереди означает большую жесткость пружины. А при этом возникает так называемый параметрический резонанс (вызванный соотношением параметров модели k1 и k2) и колебания с возрастающей амплитудой. Не помогут тот ни интуиция, ни графики. Только формулы дадут точный ответ, что будет происходить.
А на графике уже потом можно будет показать, что будет примерно так:

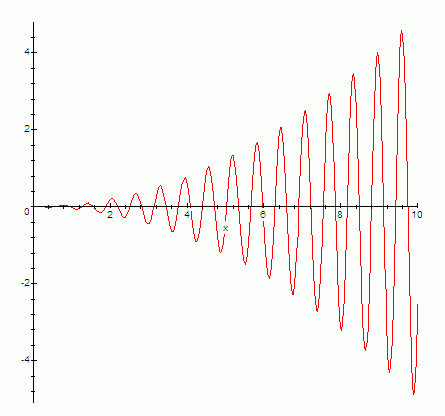
Именно на этом недостатке визуальных средств для работы с информацией и начал возникать и развиваться математический анализ как, по сути, ещё один «глаз», позволяющий смотреть на информацию. Он необычен. Никакой житейский опыт этот механизм восприятие не тренирует. Это чистая конструкция внутри сознания, которую можно соорудить и развить. И даже можно приучиться пользоваться именно ею в первую очередь, а не глазами.
Здесь я писала про то, что похожее явление может быть нарисовано разными функциями:
http://akostina76.ucoz.ru/blog/2017-02-18-3865

… но очень важно знать, что там на самом деле. Это привычно отработал возникший на первых двух курсах «математический глаз». Именно там и тогда удалось навсегда запомнить, что похожее - не одинаковое, хотя бы потому, что площадь под одними убывающими функциями конечна, а под другими (пусть и похожими) бесконечна, а это принципиально важное отличие, при том, что это отличие невозможно увидеть глазами.
Это такая привычка смотреть не глазами, а мозгами, ощупывать информацию формулами, и именно там видеть зависимости и находить ответы.
В значках нет ничего сложного. Их не так много:

Нет никакого специального знака для типового «заклинания» из конспектов «обр.отобр. непр.диф», означающего «обратное отображение непрерывно дифференцируемо», но хотя бы часть слов заменена на такие значки.
В конспектах каждый волен писать что угодно. Вот ещё парочка:

«!» означающей «единственная» в фразе:

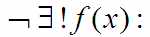
- т.е «пусть существует единственная f(x) такая что». Видимо в восклицательный знак переделали близкую по смыслу единицу.
А таким схематичным изображением глаза можно заменить слово «рассмотрим»:

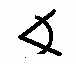
… которое тоже часто звучит на лекциях.
Проблема тут не в обозначениях как порождении конспектов а в самой логике. Мозг должен преобразовывать информацию от «фотоэлементов» в глазах в понятие «зелёный» и объект «лист растения». Какие-то нейронные цепочки должны научиться работать с информацией, поступающей в неком виде и преобразовать её в понятия и даже выводы. Как мозг определяет что «нечто» это лист растения? Небольшое, сплошное, на круг похоже, но не круг, обычно вытянуто с двух противоположных сторон. Если цветовое пятно такого вида то (логический вывод!) передо мной лист.
Из Фихтенгольц «Курс дифференциального и интегрального исчисления», стр 46:
|
Это начало, возникновение той конструкции, того «глаза», которым надо смотреть на информацию. Почему тут «варианта», а не «последовательность» я не знаю. Последовательность – варианта это вот это:

… т.е это некий набор информации, точное название которого не особо важно. Но именно с этим (как глазам со световым потоком) придётся работать. Выше было дано определение предела. Вот назвали свет с длиной волны 500-565нм зелёным и теперь в «мире» цветового восприятия возник свой внутренний закон-определение «500-565нм=зелёный».
Придумали некую область ε для хоть какой-то визуализации информации. Можно нарисовать так:

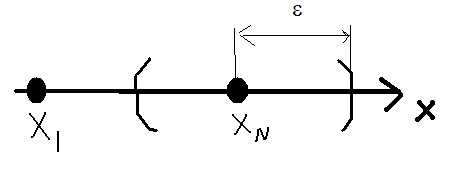
Это уже схема того самого «бесконечно малого», которое никто никогда не увидит. Тут уже возникла сколь угодно малая окрестность предела Xn и утверждение, что X1 может быть где угодно, т.е и за её пределами, но существует некоторый достаточно большой номер N при котором все Xn уже не вылезут из этой сколь угодно малой области.
«Зелёный» - абстрактное понятие потому человек может придумать «салатный» или «травяной» чтобы объяснить сложное с помощью обыденных примеров и понятий. Вот и у меня получилось «бесконечно малое» шириной во весь экран. Но вот картинки-то обычно и не рисуют. Цель как раз уйти от них.
А это определение бесконечно малого:

… т. е такой же плод фантазии как выше данное определение предела и придуманные человеком названия цветов. В этом «мире» всё, что будет болтаться конкретно возле нуля теперь смело можно называть бесконечно малыми. Это такой «закон» этого «мира».
Дальше появятся ещё какие-то определения. Будут строиться логические цепочки.
Здесь:
http://akostina76.ucoz.ru/blog/2017-03-16-3954

… я с помощью глаз могу увидеть, что левее стрелки графики похожи:

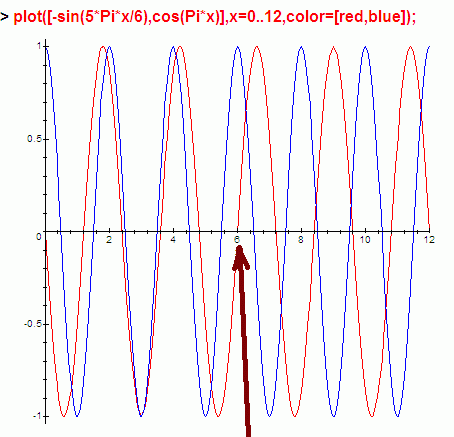
…Я делаю этот вывод из близости расположения точек разного цвета. Математический анализ даёт возможность точно говорить о близости, например, точек не рисуя графики.
Здесь я пишу про то, что интеграл можно приблизить хоть прямоугольниками, хоть трапециями, хоть параболами:
http://akostina76.ucoz.ru/blog/2017-03-17-3956

… а ширину «столбика» можно выбрать «на глаз». А если не на глаз? Если мне всё-таки очень хочется потратить минимум времени и получить максимум точности, то какой интервал мне нужен при каждом методе?
Если очень хочется, то можно и «глазами» посчитать сколько точек – пикселей у меня потеряется при методе вычисления трапециями:

Но ведь это же смешно. Нужно что-то надежнее, проще и быстрее. Математика при всей её реальной сложности даёт инструментарий для таких точных расчетов. При этом это действительно проще для тех задач, которые возникли уже очень давно а со временем только усложнились. Численные методы, программирование это же тоже по сути математика, её продолжение туда где аналитические методы уже не работаёт. Просто произошло следующее усложнение задач и оно потребовало развития инструментов этого типа, тогда как понятие пределов и бесконечно малых придумали во времена Ньютона или чуть позже (потому что в тот момент тоже возникла потребность в специфических инструментах для работы, без которых было никак).
Вот эту особую логику, умение преобразовывать «длины световых волн в цвета» и делать выводы о равенстве и отличии сложно осваивать. Тут свое «очевидно» и «сомнительно», «доказано» и «не доказано». Мозги – «пальцы»  не сразу научаются делать выводы по результатам «ощупывания» информации этим «рецептором».
При этом поскольку это свой «мир» (причём довольно большой), то есть люди, которые «селятся» именно там и их мало интересуют физические применения инструментария. Точно также программистам, которые пишут операционные системы просто по человечески не интересны бухгалтерские отчёты и оптимальное расположение кнопок на экране. Обратная ситуация это когда бухгалтер не способен запустить антивирусник.  Гипертрофированное и то и другое довольно плохо, но так бывает. И отличия в интересах объективно существует при том, что люди, формально работают с одним и тем же (компьютером, физическими явлениями).