Вывод волнового уравнения для перемещений струны

Решение волнового уравнения получено. Что-то там меняется со временем. И то, насколько часто это меняется зависит от константы «a». Для одного случая физический смысл константы «a» уже известен.
В случае бегущих по струне/стержню волн сжатия и растяжения:
http://akostina76.ucoz.ru/blog/2017-02-09-3836

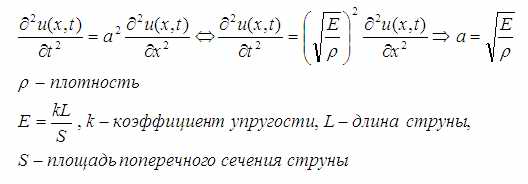
Аналогичное по форме уравнение можно получить и для колебания струны, точнее для перемещений точек струны во времени.
Струной считается вовсе не всё, что закреплено и изогнуто:
plot([0.1*sin(x),sin(x)],x=0..Pi,scaling=constrained);

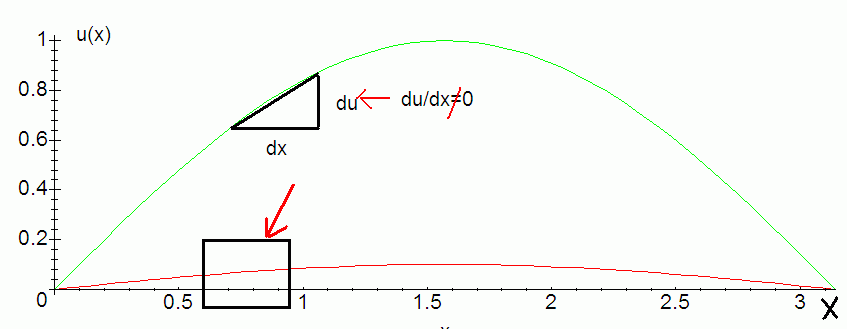
Здесь например снизу (красное) это струна, а сверху (зелёное) это не струна потому что прогиб слишком велик. Такое большое отклонение не даёт возможность считать u’(x) =du/dx примерно равным нулю и пренебрегать им в расчетах (а дальше будет делаться именно это).
Кусок струны в маленьком прямоугольнике выглядит так:

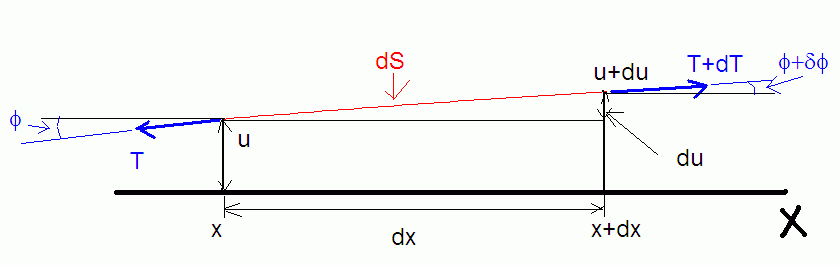
Во-первых, у него есть (понятно что малая) длина dS. Во-вторых, отклонения слева (u) не равно отклонению справа (u+du). Это отклонение u(x,t). т. е меняющееся и со временем и в разных точка струны и будет искомым «u» волнового уравнения. В-третьих, это же не просто так кусок материала в воздухе. За этот кусок тянут с двух сторон некие силы остальной струны, которые вообще-то не обязаны быть равны. Потому слева эта сила равна T, а справа – T+dT. Тянут эти силы под углами, касательными к изгибу струны в этих точках. Эти углы (φ и φ+dφ) тоже естественно какие-то, неизвестные и не обязанные быть равными (потому и записано, что они отличаются на какое-то dφ).
Всё тут мало, потому по теореме Пифагора можно сказать, что квадрат длины куска струны dS (гипотенуза) равен сумме квадратов катетов dx*dx+du*du. Но струной я считаю только то, что имеет очень малый наклон. А это означает что du*du настолько малая величина, что ей можно отбросить и считать, что dS=dx.
Дальше, как во многих механических задачах полагается расписать проекции действующих сил на координатные оси X и Y.
Для этого надо вспомнить основное для чего на практике используются синусы и косинусы:
http://akostina76.ucoz.ru/blog/2017-02-16-3858

… т.е как раз для выражения этих проекций через угол и гипотенузу. Рисовать на правом конце отрезка не очень удобно, но там так:

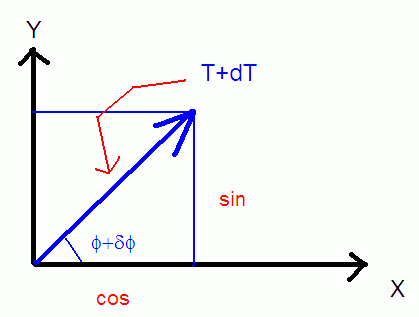
Проекция силы – гипотенузы T+dT на ось Y выражается через синус:
 
А проекция на ось X через косинус:
 

Тоже самое можно написать на левом конце струны, т.е там где сила равна T, а угол равен φ.
Я считаю, что у меня смещения по Y малы, а смещений по оси X вообще не происходит. Т.е вот такие перемещения бывает:

А такие, как я считаю (при малых смещениях даже по Y) не бывает:

Они, конечно, тоже есть. Но они настолько малы, что можно считать, что их нет. Вот я и считаю. А раз я считаю, что их нет (т.е нет перемещения по оси X) для проекций на эту ось я могу записать так:
T*cos(φ)=(T+dT)* cos(φ+dφ)
или так, чтобы подчеркнуть, что перемещения нет (т.е оно = 0):
(T+dT)* cos(φ+dφ)- T*cos(φ)=0
Я считаю, что угол φ у меня мал по всё той же причине малых отклонений. Косинус примерно нуля – примерно 1. Это означает, что я эти косинусы вообще могу отбросить заменив единицами. Будет так:
T+dT-T=0 => dT=0 =>T=const.
В результате всех этих рассуждений у меня получилось что сила T одинакова по величине и справа и слева. Оно и логично. Ведь я решила что у меня нет сдвига ни влево ни вправо. А так может быть только при равенстве тащащих в разные стороны сил.
А вот перемещение по оси Y у меня есть и пусть пока не важно, чему оно там равно. Пусть это будет W(x,t). Тогда для проекции на ось Y будет записано так:
(T+dT)* sin(φ+dφ)-T*sin(φ) =W(x,t)
Но тут у меня всё тот же малый угол φ. Если выше я отбросила его косинус заменив единицей, то ничто не мешает мне здесь заменить единицу на косинус:

В результате возникли два тангенса (в начале и в конце отрезка, т.е при x и x+dx). А тангенсы это отношения приращений функции к её аргументу, т.е это просто определение производной функции в некой точке. Т.е в результате у меня получилось два значения производных (от функции u) в двух точках  (x и x+dx). После этого я вспомнила о том, что T у меня постоянно (из первого уравнения)  и отбросила равное нулю dT. Получилось то, что получилось.
По второму закону Ньютона F=m*a, где «F» – сила, вызвавшая движение, «m»– масса, «а» - ускорение, т.е вторая производная по времени. F – это только что полученная результирующая сила, а m*a это то самое W(x,t).
Всё вместе так:


Для практического применения важно, что ρ это не обычная плотность, а погонная, т.е масса на единицу длины (т.е обычная плотность умноженная на площадь сечения). Всё подставлено и приравнено. dx можно и нужно перенести из правой части в левую. Деление разности, которая там есть, на dx даст вторую производную (тоже просто по определению второй производной функции). Перенос констант дал физический смысл «a» для отклонений струны.